{ 
[n:
]
[A:n 
Type]. [m:]. [B:m Type]. [T:Type]. [f:i:n (A i + Top)
i:m
(B i + Top)
T].
(modify-combinator1(f) 
i:n - 1 if (i =
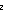0)
then one_or_both(A 0;A 1) + Top
else A (i + 1) + Top
fi
i:m (B i + Top)
T)
supposing 1 < n }
{ Proof }
Definitions occuring in Statement :
modify-combinator1: modify-combinator1(f),
eq_int: (i =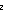 j),
ifthenelse: if b then t else f fi ,
int_seg: {i..j
},
nat: ,
uimplies: b supposing a,
uall: [x:A]. B[x],
top: Top,
member: t T,
less_than: a < b,
apply: f a,
function: x:A B[x],
union: left + right,
subtract: n - m,
add: n + m,
natural_number: $n,
universe: Type,
one_or_both: one_or_both(A;B)
Definitions :
deq: EqDecider(T),
ma-state: State(ds),
class-program: ClassProgram(T),
fpf-cap: f(x)?z,
it: 
,
eq_knd: a = b,
fpf-dom: x dom(f),
eq_bool: p =b q,
IdLnk: IdLnk,
Id: Id,
append: as @ bs,
locl: locl(a),
Knd: Knd,
list: type List,
lt_int: i <z j,
le_int: i 
z j,
limited-type: LimitedType,
pair: <a, b>,
btrue: tt,
iff: P 
Q,
eq_atom: x =a y,
null: null(as),
set_blt: a <
b,
grp_blt: a < b,
infix_ap: x f y,
dcdr-to-bool: [d],
bl-all: (xL.P[x])_b,
bl-exists: (
xL.P[x])_b,
b-exists: (i<n.P[i])_b,
eq_type: eq_type(T;T'),
eq_atom: eq_atom$n(x;y),
qeq: qeq(r;s),
q_less: q_less(r;s),
q_le: q_le(r;s),
deq-member: deq-member(eq;x;L),
deq-disjoint: deq-disjoint(eq;as;bs),
deq-all-disjoint: deq-all-disjoint(eq;ass;bs),
eq_str: Error :eq_str,
eq_id: a = b,
eq_lnk: a = b,
es-eq-E: e = e',
bimplies: p q,
band: p 
q,
bor: p 
q,
bnot: 
b,
inr: inr x ,
unit: Unit,
oob-getright: oob-getright(x),
oob-hasright: oob-hasright(x),
sq_stable: SqStable(P),
so_apply: x[s],
or: P Q,
l_member: (x l),
guard: {T},
sq_type: SQType(T),
true: True,
decision: Decision,
assert: 
b,
bfalse: ff,
oob-getleft: oob-getleft(x),
inl: inl x ,
oob-hasleft: oob-hasleft(x),
bool: 
,
p-outcome: Outcome,
minus: -n,
void: Void,
rationals: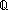 
,
decide: case b of inl(x) => s[x] | inr(y) => t[y],
lelt: i j < k,
lambda: 
x.A[x],
real: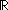 
,
grp_car: |g|,
subtype: S 
T,
fpf: a:A fp-> B[a],
strong-subtype: strong-subtype(A;B),
ge: i 
j ,
product: x:A 
B[x],
and: P Q,
uiff: uiff(P;Q),
subtype_rel: A r B,
all: x:A. B[x],
implies: P Q,
false: False,
not: A,
le: A B,
int: 
,
set: {x:A| B[x]} ,
axiom: Ax,
modify-combinator1: modify-combinator1(f),
add: n + m,
one_or_both: Error :one_or_both,
eq_int: (i =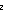 j),
ifthenelse: if b then t else f fi ,
subtract: n - m,
natural_number: $n,
top: Top,
apply: f a,
union: left + right,
equal: s = t,
uimplies: b supposing a,
prop: 
,
less_than: a < b,
nat: ,
uall: [x:A]. B[x],
universe: Type,
int_seg: {i..j},
function: x:A B[x],
member: t T,
isect: 
x:A. B[x],
squash: 
T,
so_lambda: 
x.t[x],
sqequal: s ~ t,
MaAuto: Error :MaAuto,
Unfold: Error :Unfold,
CollapseTHEN: Error :CollapseTHEN,
Auto: Error :Auto,
tactic: Error :tactic
Lemmas :
set_subtype_base,
subtype_base_sq,
int_subtype_base,
squash_wf,
top_wf,
int_seg_properties,
eq_int_wf,
ifthenelse_wf,
int_seg_wf,
nat_wf,
member_wf,
le_wf,
not_wf,
false_wf,
nat_properties,
Error :one_or_both_wf,
oob-hasleft_wf,
oob-getleft_wf,
assert_wf,
true_wf,
subtype_rel_wf,
bfalse_wf,
bool_wf,
oob-hasright_wf,
oob-getright_wf,
iff_weakening_uiff,
uiff_transitivity,
eqtt_to_assert,
assert_of_eq_int,
eqff_to_assert,
assert_of_bnot,
not_functionality_wrt_uiff,
bnot_wf
\mforall{}[n:\mBbbN{}]
\mforall{}[A:\mBbbN{}n {}\mrightarrow{} Type]. \mforall{}[m:\mBbbN{}]. \mforall{}[B:\mBbbN{}m {}\mrightarrow{} Type]. \mforall{}[T:Type]. \mforall{}[f:i:\mBbbN{}n {}\mrightarrow{} (A i + Top)
{}\mrightarrow{} i:\mBbbN{}m {}\mrightarrow{} (B i + Top)
{}\mrightarrow{} T].
(modify-combinator1(f) \mmember{} i:\mBbbN{}n - 1 {}\mrightarrow{} if (i =\msubz{} 0)
then one\_or\_both(A 0;A 1) + Top
else A (i + 1) + Top
fi
{}\mrightarrow{} i:\mBbbN{}m {}\mrightarrow{} (B i + Top)
{}\mrightarrow{} T)
supposing 1 < n
Date html generated:
2011_08_16-AM-11_04_04
Last ObjectModification:
2011_06_18-AM-09_37_02
Home
Index