Thm*  n:{1...}. n:{1...}.
Thm* 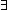 h:({2..(n+1) h:({2..(n+1) } }   ). ).
Thm* n =   {2..n+1 {2..n+1 }(h) & is_prime_factorization(2; (n+1); h) }(h) & is_prime_factorization(2; (n+1); h) | [prime_factorization_exists] |
Thm*  k:{2...}, n: k:{2...}, n: , g:({2..k , g:({2..k } }   ). ).
Thm* 2 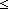 n < k+1 n < k+1
Thm*  
Thm* ( i:{2..k i:{2..k }. n }. n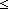 i i   0<g(i) 0<g(i)   prime(i)) prime(i))
Thm*  
Thm* (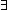 h:({2..k h:({2..k } }   ). ).
Thm* (  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(h) & is_prime_factorization(2; k; h)) }(h) & is_prime_factorization(2; k; h)) | [prime_factorization_existsLEMMA] |
Thm*  k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), z:{2..k ), z:{2..k }. }.
Thm* 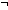 prime(z) prime(z)
Thm*  
Thm* (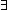 g':({2..k g':({2..k } }   ). ).
Thm* (  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(g') }(g')
Thm* (& g'(z) = 0
Thm* (& ( u:{2..k u:{2..k }. z<u }. z<u   g'(u) = g(u))) g'(u) = g(u))) | [can_reduce_composite_factor2] |
Thm*  k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x,y:{2..k ), x,y:{2..k }. }.
Thm* x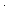 y<k y<k
Thm*  
Thm* (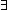 h:({2..k h:({2..k } }   ). ).
Thm* (  {2..k {2..k }(g) = }(g) =   {2..k {2..k }(h) }(h)
Thm* (& h(x y) = 0 y) = 0
Thm* (& ( u:{2..k u:{2..k }. x }. x y<u y<u   h(u) = g(u))) h(u) = g(u))) | [can_reduce_composite_factor] |
Thm*  k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x:{2..k ), x:{2..k }. }.
Thm* x x<k x<k
Thm*  
Thm*   {2..k {2..k }(g) = }(g) =   {2..k {2..k }(split_factor1(g; x)) }(split_factor1(g; x))
Thm* & split_factor1(g; x)(x x) = 0 x) = 0
Thm* & ( u:{2..k u:{2..k }. x }. x x<u x<u   split_factor1(g; x)(u) = g(u)) split_factor1(g; x)(u) = g(u)) | [split_factor1_char] |
Thm*  k:{2...}, g:({2..k k:{2...}, g:({2..k } }   ), x,y:{2..k ), x,y:{2..k }. }.
Thm* x y<k y<k
Thm*  
Thm* x<y
Thm*  
Thm*   {2..k {2..k }(g) = }(g) =   {2..k {2..k }(split_factor2(g; x; y)) }(split_factor2(g; x; y))
Thm* & split_factor2(g; x; y)(x y) = 0 y) = 0
Thm* & ( u:{2..k u:{2..k }. x }. x y<u y<u   split_factor2(g; x; y)(u) = g(u)) split_factor2(g; x; y)(u) = g(u)) | [split_factor2_char] |
Thm*  a:{2...}, b: a:{2...}, b: , g,h:({a..b , g,h:({a..b } }   ). ).
Thm* is_prime_factorization(a; b; g)
Thm*  
Thm* is_prime_factorization(a; b; h)     {a..b {a..b }(g) = }(g) =   {a..b {a..b }(h) }(h)   g = h g = h | [prime_factorization_unique] |
Thm*  a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
Thm* is_prime_factorization(a; b; f)
Thm*  
Thm* prime(p)
Thm*  
Thm* p |   {a..b {a..b }(f) }(f)     {a..b {a..b }(f) = p }(f) = p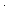   {a..b {a..b }(reduce_factorization(f; p)) }(reduce_factorization(f; p)) | [remove_prime_factor] |
Thm*  a: a: , b: , b: , f:({a..b , f:({a..b } }   ), p: ), p: . .
Thm* is_prime_factorization(a; b; f)
Thm*  
Thm* prime(p)   p | p |   {a..b {a..b }(f) }(f)   p p 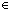 {a..b {a..b } & 0<f(p) } & 0<f(p) | [prime_factorization_includes_prime_divisors] |
Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. 0<f(j) }. 0<f(j)   j | j |   {a..b {a..b }(f) }(f) | [factor_divides_evalfactorization] |
Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ). b ). b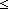 a a     {a..b {a..b }(f) = }(f) =   {a..a {a..a }(f) }(f) | [eval_factorization_nullnorm] |
Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ). b ). b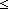 a a     {a..b {a..b }(f) = 1 }(f) = 1 | [eval_factorization_intseg_null] |
Thm*  a: a: 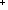 , b: , b: , f:({a..b , f:({a..b } }   ), j:{a..b ), j:{a..b }. }.
Thm* 2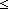 j j   0<f(j) 0<f(j)     {a..b {a..b }(reduce_factorization(f; j))< }(reduce_factorization(f; j))<  {a..b {a..b }(f) }(f) | [eval_reduce_factorization_less] |
Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ), z:{a..b ), z:{a..b }. }.
Thm* 0<f(z)     {a..b {a..b }(f) = z }(f) = z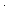   {a..b {a..b }(reduce_factorization(f; z)) }(reduce_factorization(f; z)) | [eval_factorization_pluck] |
Thm*  a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ). ).
Thm*   {a..b {a..b }(f) }(f)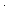   {a..b {a..b }(g) = }(g) =   {a..b {a..b }( }(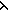 i.f(i)+g(i)) i.f(i)+g(i)) | [eval_factorization_prod] |
Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).
Thm* 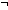   {a..b {a..b }(f) = 1 }(f) = 1 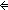  ( (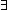 i:{a..b i:{a..b }. }. 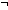 f(i) = 0) f(i) = 0) | [eval_factorization_not_one] |
Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 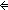  f = ( f = (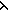 x.0) x.0) | [eval_factorization_one_c] |
Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 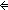  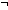 ( (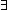 i:{a..b i:{a..b }. 0<f(i)) }. 0<f(i)) | [eval_factorization_one_b] |
Thm*  a:{2...}, b: a:{2...}, b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) = 1 }(f) = 1 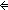  ( ( i:{a..b i:{a..b }. f(i) = 0) }. f(i) = 0) | [eval_factorization_one] |
Thm*  a: a: 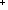 , b: , b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) }(f) 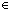  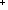 | [eval_factorization_nat_plus] |
Thm*  a,b: a,b: , j:{a..b , j:{a..b }. }.   {a..b {a..b }(trivial_factorization(j)) = j }(trivial_factorization(j)) = j | [eval_trivial_factorization] |
Thm*  a,c,b: a,c,b: , f:({a..b , f:({a..b } }   ). ).
Thm* a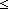 c c   c<b c<b     {a..b {a..b }(f) = }(f) =   {a..c {a..c }(f) }(f)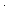 c c f(c) f(c)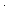   {c+1..b {c+1..b }(f) }(f) | [eval_factorization_split_pluck] |
Thm*  a,c,b: a,c,b: , f:({a..b , f:({a..b } }   ). ).
Thm* a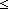 c c   c c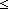 b b     {a..b {a..b }(f) = }(f) =   {a..c {a..c }(f) }(f)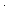   {c..b {c..b }(f) }(f) | [eval_factorization_split_mid] |
Def f is a factorization of k
Def == ( x:Prime x:Prime . k<x . k<x   f(x) = 0) & k = f(x) = 0) & k =   {2..k+1 {2..k+1 }(prime_mset_complete(f)) }(prime_mset_complete(f)) | [prime_factorization_of] |