At: auto2 lemma 3 1 1 1 2 1 1 1
1. Alph: Type
2. R: Alph*
Alph*Prop
3. n: 
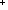
4. 
x:Alph*. R(x,x)
5. x,y:Alph*. R(x,y) 
R(y,x)
6. x,y,z:Alph*. R(x,y) & R(y,z) R(x,z)
7. x,y,z:Alph*. R(x,y) R((z @ x),z @ y)
8. w: nAlph*
9. l:Alph*. 
i:n. R(l,w(i))
10. a: Alph*
11. b: Alph*
12. c: Alph*
13. ||a||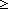
n
n
14. f: Alph*n
15. x:Alph*. R(x,w(f(x)))
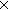
16. f1: n
n(nn)
17. Bij(nn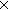; (nn); f1)
18. i: (nn+1)
19. j: (nn+1)
20. i < j
21. f1( < f((a[||a||-i..||a||
]) @ b),f((a[||a||-i..||a||]) @ c) > )
=
f1( < f((a[||a||-j..||a||]) @ b),f((a[||a||-j..||a||]) @ c) > )
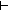||(a[0..||a||-j]) @ (a[||a||-i..||a||])|| < ||a||
By:
RWH
(LemmaC
Thm* as,bs:T*. ||as @ bs|| = ||as||+||bs||)
0
THEN
RWH
(LemmaC
Thm* as:T*, i:{0...||as||}, j:{i...||as||}. ||as[i..j]|| = j-i)
0
Generated subgoals:None
About:
