| 1 | 17. Inj( n n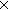  n; n;  (n (n n); f1) & Surj( n); f1) & Surj( n n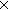  n; n;  (n (n n); f1) n); f1)
18. i:  (n (n n+1) n+1)
19. j:  (n (n n+1) n+1)
20. i < j
21. f1( < f((a[||a||-i..||a|| ]) @ b),f((a[||a||-i..||a|| ]) @ b),f((a[||a||-i..||a|| ]) @ c) > )
=
f1( < f((a[||a||-j..||a|| ]) @ c) > )
=
f1( < f((a[||a||-j..||a|| ]) @ b),f((a[||a||-j..||a|| ]) @ b),f((a[||a||-j..||a|| ]) @ c) > ) ]) @ c) > )
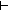 R((a @ b),((a[0..||a||-j R((a @ b),((a[0..||a||-j ]) @ (a[||a||-i..||a|| ]) @ (a[||a||-i..||a|| ])) @ b)
& R((a @ c),((a[0..||a||-j ])) @ b)
& R((a @ c),((a[0..||a||-j ]) @ (a[||a||-i..||a|| ]) @ (a[||a||-i..||a|| ])) @ c) ])) @ c) |