| 1 | 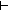 ( (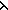 x.if x= x.if x=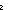 m m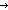 f(n-1) else f1(x) fi) f(n-1) else f1(x) fi) 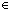  (m+1) (m+1)  {t:T| B(t) } {t:T| B(t) } |
| 2 | 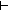  (m+1) (m+1)  {t:T| B(t) } {t:T| B(t) } 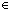 Type{[1 | i 0]} Type{[1 | i 0]} |
| 3 | 18. f2:  (m+1) (m+1)  {t:T| B(t) } {t:T| B(t) }
19. f2 = (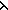 x.if x= x.if x=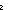 m m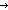 f(n-1) else f1(x) fi) f(n-1) else f1(x) fi)
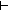 ( (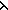 x.if g(x)= x.if g(x)=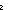 n-1 n-1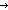 m else g@0(x) fi) m else g@0(x) fi) 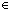 {t:T| B(t) } {t:T| B(t) }   (m+1) (m+1) |
| 4 | 18. f2:  (m+1) (m+1)  {t:T| B(t) } {t:T| B(t) }
19. f2 = (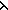 x.if x= x.if x=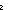 m m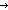 f(n-1) else f1(x) fi) f(n-1) else f1(x) fi)
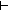 {t:T| B(t) } {t:T| B(t) }   (m+1) (m+1) 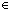 Type{[1 | i 0]} Type{[1 | i 0]} |
| 5 | 18. f2:  (m+1) (m+1)  {t:T| B(t) } {t:T| B(t) }
19. f2 = (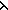 x.if x= x.if x=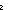 m m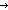 f(n-1) else f1(x) fi) f(n-1) else f1(x) fi)
20. g2: {t:T| B(t) }   (m+1) (m+1)
21. g2 = (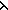 x.if g(x)= x.if g(x)=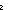 n-1 n-1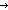 m else g@0(x) fi) m else g@0(x) fi)
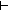  m: m: , f:( , f:( m m  {t:T| B(t) }), g:({t:T| B(t) } {t:T| B(t) }), g:({t:T| B(t) }   m). InvFuns( m). InvFuns( m; {t:T| B(t) }; f; g) m; {t:T| B(t) }; f; g) |