| 1 | 7. f(i) = n-1
8. f(j) = n-1
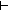 f(n) = f(n) f(n) = f(n) 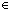  (-1+n) (-1+n)   ( ( i: i: 1, j: 1, j: i. f(i) = f(j)) i. f(i) = f(j)) |
| 2 | 7. f(i) = n-1
8. 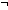 f(j) = n-1 f(j) = n-1
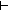 f(n) = f(j) f(n) = f(j) 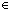  (-1+n) (-1+n)   ( ( i: i: 1, j: 1, j: i. f(i) = f(j)) i. f(i) = f(j)) |
| 3 | 7. 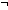 f(i) = n-1 f(i) = n-1
8. f(j) = n-1
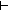 f(i) = f(n) f(i) = f(n) 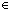  (-1+n) (-1+n)   ( ( i: i: 1, j: 1, j: i. f(i) = f(j)) i. f(i) = f(j)) |
| 4 | 7.  f(i) = n-1 f(i) = n-1
8.  f(j) = n-1 f(j) = n-1
 f(i) = f(j) f(i) = f(j)   (-1+n) (-1+n)   ( ( i: i: 1, j: 1, j: i. f(i) = f(j)) i. f(i) = f(j)) |