| 1 |
7. f :  ||L|| ||L||   ||L|| ||L||
8.  i: i: ||L||. f(i) = (n, n+1)(i) ||L||. f(i) = (n, n+1)(i)
 sum(if (i< sum(if (i<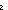 j) j)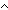 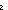 P(swap(L;n;n+1)[i],swap(L;n;n+1)[j]) P(swap(L;n;n+1)[i],swap(L;n;n+1)[j])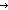 1 1
 sum(else 0 fi | i < ||L||; j < ||L||) sum(else 0 fi | i < ||L||; j < ||L||)
 = =
 sum(if (i< sum(if (i<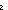 j) j)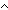 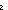 P(L[i],L[j]) P(L[i],L[j])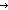 1 else 0 fi | i < ||L||; j < ||L||)+if P(L[n] 1 else 0 fi | i < ||L||; j < ||L||)+if P(L[n]
 sum(if (i< sum(if (i< j) j)  P(L[i],L[j]) P(L[i],L[j]) 1 else 0 fi | i < ||L||; j < ||L||)+if P,L[(n 1 else 0 fi | i < ||L||; j < ||L||)+if P,L[(n
 sum(if (i< sum(if (i< j) j)  P(L[i],L[j]) P(L[i],L[j]) 1 else 0 fi | i < ||L||; j < ||L||)+if P+1)]) 1 else 0 fi | i < ||L||; j < ||L||)+if P+1)])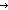
 sum(if (i< sum(if (i< j) j)  P(L[i],L[j]) P(L[i],L[j]) 1 else 0 fi | i < ||L||; j < ||L||)+if -1 1 else 0 fi | i < ||L||; j < ||L||)+if -1
 sum(if (i< sum(if (i< j) j)  P(L[i],L[j]) P(L[i],L[j]) 1 else 0 fi | i < ||L||; j < ||L||)+else 0 fi 1 else 0 fi | i < ||L||; j < ||L||)+else 0 fi
 +if P(L[(n+1)],L[n]) +if P(L[(n+1)],L[n])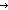 1 else 0 fi 1 else 0 fi
 | 25 steps |