At: nd ext valcom 1 1 2 1 1 1 1 1 1 1 2 1 2 1
1. Alph: Type
2. St: Type
3. NDA: NDA(Alph;St)
4. C: (St Alph*)*
Alph*)*
5. ||C|| > 0
6.  i:
i: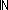 (||C||-1). ||2of(C[i])|| > 0
(||C||-1). ||2of(C[i])|| > 0
7. q: St
8. a: Alph
9. p: St
10. NDA(C)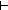 q
q
11. 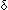 NDA(q,a,p)
NDA(q,a,p)
12. i: 
13. 0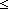 i
i
14. i < ||map( c. < 1of(c),a.2of(c) > ;C)||+1-1
c. < 1of(c),a.2of(c) > ;C)||+1-1
15. 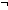 i = ||C||-1
i = ||C||-1
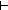 ||2of(map(
||2of(map( c. < 1of(c),a.2of(c) > ;C)[i])||
c. < 1of(c),a.2of(c) > ;C)[i])||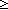 1
1
By:
RWH
(LemmaC
Thm*  f:(A
f:(A
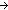 B), as:A*, n:
B), as:A*, n: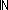 ||as||. map(f;as)[n] = f(as[n]))
0
||as||. map(f;as)[n] = f(as[n]))
0
THEN
Reduce 0
Generated subgoal:| 1 | 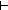 ||2of(C[i])||+1 ||2of(C[i])||+1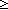 1 1 |
About: