Nuprl Lemma : surject_implies_decidble_eq2
T:Type. ((
f:
T. Surj(;T;f)) 
(t1,t2:T. Dec(t1 = t2)))
Proof
Definitions occuring in Statement :
surject: Surj(A;B;f),
nat: ,
decidable: Dec(P),
all: x:A. B[x],
exists: x:A. B[x],
implies: P Q,
function: x:A B[x],
universe: Type,
equal: s = t
Definitions :
so_lambda: 
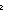x.t[x],
member: t 
T,
decidable: Dec(P),
implies: P Q,
all: x:A. B[x],
prop: 
,
subtype: S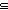 
T,
top: Top,
exists: x:A. B[x],
nat: ,
pi1: fst(t),
or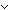: P 
Q,
and: P 
Q,
guard: {T},
not: 
A,
so_apply: x[s],
uall: [x:A]. B[x],
surject: Surj(A;B;f),
uimplies: b supposing a,
sq_type: SQType(T)
Lemmas :
surject_wf,
nat_wf,
exists_wf,
all_wf,
equal_wf,
pi1_wf_top,
int_subtype_base,
le_wf,
set_subtype_base,
subtype_base_sq,
decidable__equal_nat,
not_wf,
and_wf
\mforall{}T:Type. ((\mexists{}f:\mBbbN{} {}\mrightarrow{} T. Surj(\mBbbN{};T;f)) {}\mRightarrow{} (\mforall{}t1,t2:T. Dec(t1 = t2)))
Date html generated:
2013_03_20-AM-09_48_22
Last ObjectModification:
2012_11_27-AM-10_32_01
Home
Index