Nuprl Lemma : vr_divKplus
n,m:
. k:
. (((n + (k * m))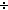 
k) = ((n 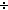k) + m))
Proof not projected
Definitions occuring in Statement :
nat_plus: ,
nat: ,
all: x:A. B[x],
divide: n 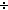m,
multiply: n * m,
add: n + m,
int: 
,
equal: s = t
Definitions :
tactic: Error :tactic,
THENA: Error :THENA,
Auto: Error :Auto,
all: x:A. B[x],
function: x:A 
B[x],
nat_plus: ,
nat: ,
member: t 
T,
equal: s = t,
subtract: n - m,
minus: -n,
prop: 
,
uall: [x:A]. B[x],
isect: 
x:A. B[x],
subtype: S 
T,
int: ,
grp_car: |g|,
less_than: a < b,
implies: P 
Q,
le: A 
B,
ge: i 
j ,
add: n + m,
divide: n 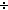m,
real: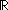 
,
set: {x:A| B[x]} ,
multiply: n * m,
int_nzero: 
,
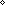nequal: a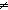 
b T ,
not: 
A,
false: False,
void: Void,
natural_number: $n,
THEN: Error :THEN,
uimplies: b supposing a,
rationals: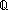 
,
subtype_rel: A r B,
uiff: uiff(P;Q),
and: P 
Q,
product: x:A 
B[x],
strong-subtype: strong-subtype(A;B),
universe: Type,
length: ||as||,
CollapseTHEN: Error :CollapseTHEN,
exists: 
x:A. B[x],
limited-type: LimitedType,
sq_type: SQType(T),
guard: {T},
rev_implies: P 
Q,
iff: P Q,
squash: 
T,
true: True,
D: Error :D
Lemmas :
add_ident,
add_functionality_wrt_eq,
true_wf,
squash_wf,
rev_implies_wf,
iff_wf,
int_subtype_base,
subtype_base_sq,
nat_plus_inc,
mul_bounds_1a,
vr_add_ge_zero,
false_wf,
not_wf,
le_wf,
member_wf,
div_rec_case,
nat_ind_tp,
nat_properties,
ge_wf,
nat_wf,
nat_plus_wf
\mforall{}n,m:\mBbbN{}. \mforall{}k:\mBbbN{}\msupplus{}. (((n + (k * m)) \mdiv{} k) = ((n \mdiv{} k) + m))
Date html generated:
2012_02_20-PM-03_32_03
Last ObjectModification:
2012_02_02-PM-01_55_04
Home
Index