{ 
[Info:Type]
es:EO+(Info). LL:Info List List. e1,e2:E.
L:Info List
(
f:
||LL|| + 1 
E
((((f 0) = e1) 
f ||LL|| 
loc e2 )
c (i:||LL||. (f i <loc f (i + 1)))
c ((i:||LL||. (es-hist(es;f i;pred(f (i + 1))) = LL[i]))
(es-hist(es;f ||LL||;e2) = L)))) supposing
((es-hist(es;e1;e2) = (concat(LL) @ L)) and
(
(L = [])) and
(L
LL.(L = [])))
supposing loc(e1) = loc(e2) }
{ Proof }
Definitions occuring in Statement :
es-hist: es-hist(es;e1;e2),
event-ordering+: EO+(Info),
es-le: e loc e' ,
es-locl: (e <loc e'),
es-pred: pred(e),
es-loc: loc(e),
es-E: E,
Id: Id,
select: l[i],
length: ||as||,
append: as @ bs,
int_seg: {i..j
},
uimplies: b supposing a,
uall: [x:A]. B[x],
cand: A c B,
all: x:A. B[x],
exists: x:A. B[x],
not: A,
and: P Q,
apply: f a,
function: x:A B[x],
nil: [],
list: type List,
add: n + m,
natural_number: $n,
universe: Type,
equal: s = t,
l_all: (xL.P[x]),
concat: concat(ll)
Definitions :
uall: [x:A]. B[x],
all: x:A. B[x],
member: t T,
uimplies: b supposing a,
l_all: (xL.P[x]),
not: A,
append: as @ bs,
concat: concat(ll),
exists: x:A. B[x],
int_seg: {i..j},
length: ||as||,
cand: A c B,
and: P Q,
reduce: reduce(f;k;as),
ycomb: Y,
implies: P 
Q,
false: False,
prop: 
,
lelt: i j < k,
le: A B,
so_lambda: 
x.t[x],
iff: P 
Q,
rev_implies: P Q,
top: Top,
subtype: S 
T,
ifthenelse: if b then t else f fi ,
btrue: tt,
bfalse: ff,
eq_int: (i =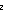
j),
squash: 
T,
true: True,
select: l[i],
le_int: i z j,
bnot: 
b,
lt_int: i <z j,
assert: 
b,
so_apply: x[s],
decidable: Dec(P),
or: P 
Q,
existse-between3: e(e1,e2].P[e],
es-locl: (e <loc e'),
bool: 
,
unit: Unit,
sq_type: SQType(T),
guard: {T},
it: 
Lemmas :
event-ordering+_wf,
l_member_wf,
int_seg_wf,
es-E_wf,
false_wf,
es-le_wf,
es-locl_wf,
int_seg_properties,
es-hist_wf,
es-pred_wf,
select_wf,
length_wf2,
not_wf,
l_all_wf2,
Id_wf,
es-loc_wf,
decidable__es-locl,
event-ordering+_inc,
null-es-hist,
assert_wf,
null_wf3,
top_wf,
iff_weakening_uiff,
assert_of_null,
es-le-not-locl,
append_wf,
concat_wf,
concat-cons,
append_assoc_sq,
es-hist-is-append,
l_all_cons,
not_functionality_wrt_uiff,
append_is_nil,
length_wf1,
eq_int_wf,
bool_wf,
bnot_wf,
uiff_transitivity,
eqtt_to_assert,
assert_of_eq_int,
eqff_to_assert,
assert_of_bnot,
non_neg_length,
length_wf_nat,
subtype_base_sq,
int_subtype_base,
le_wf,
bool_subtype_base,
es-locl-first,
squash_wf,
es-first_wf,
event_ordering_wf,
select_cons_tl_sq,
length_cons,
es-locl-iff
\mforall{}[Info:Type]
\mforall{}es:EO+(Info). \mforall{}LL:Info List List. \mforall{}e1,e2:E.
\mforall{}L:Info List
(\mexists{}f:\mBbbN{}||LL|| + 1 {}\mrightarrow{} E
((((f 0) = e1) \mwedge{} f ||LL|| \mleq{}loc e2 )
c\mwedge{} (\mforall{}i:\mBbbN{}||LL||. (f i <loc f (i + 1)))
c\mwedge{} ((\mforall{}i:\mBbbN{}||LL||. (es-hist(es;f i;pred(f (i + 1))) = LL[i]))
\mwedge{} (es-hist(es;f ||LL||;e2) = L)))) supposing
((es-hist(es;e1;e2) = (concat(LL) @ L)) and
(\mneg{}(L = [])) and
(\mforall{}L\mmember{}LL.\mneg{}(L = [])))
supposing loc(e1) = loc(e2)
Date html generated:
2011_08_16-AM-11_27_35
Last ObjectModification:
2011_06_20-AM-00_27_36
Home
Index