| Pairs
|
Thm*  B:(A B:(A  Type), p:(u:A Type), p:(u:A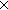 B(u)). p = <p.1,p.2> B(u)). p = <p.1,p.2>  a:A a:A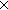 B(a) B(a)
|
| Boolean
|
Thm*  p,q: p,q: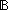 . (p . (p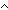 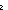 q) q) 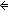  p & q p & q
|
| Unit
|
Thm*  a:Unit. a = a:Unit. a = 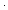
|
| Disjoint Union
|
Thm*  z:A+B. z = InjCase(z; u. inl(u); v. inr(v)) z:A+B. z = InjCase(z; u. inl(u); v. inr(v))
|
| Equality
|
Thm* (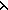 x.x) = ( x.x) = (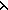 x.if x<0 x.if x<0 0 ; x fi) 0 ; x fi)     
Thm* (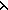 x.x) x.x) 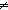 ( (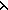 x.if x<0 x.if x<0 0 ; x fi) 0 ; x fi)     
|
| Intersection Types
|
Thm*  B:(A B:(A  Type), a:A. ( Type), a:A. (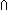 x:A. B(x)) x:A. B(x)) 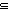 B(a) B(a)
Thm*  A:Type, B:Type(given A). A A:Type, B:Type(given A). A  B B  Type Type
|
| Quotient Types
|
Thm* 2 = 4   mod 2 mod 2
|
| Void
|
Thm* (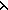 x.whatever) = ( x.whatever) = (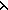 x.x) x.x)  Void Void  A A
|
| Function Types
|
Thm*  f:(A f:(A  B). ( B). (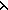 x.f(x)) = f x.f(x)) = f
Thm*  f,g:(A f,g:(A  B). f = g B). f = g 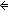  ( ( x:A. f(x) = g(x)) x:A. f(x) = g(x))
|
| Polymorphism
|
Thm*  f:(( f:(( mod 2) mod 2)  A). f A). f     A A
Thm*  T:Type, f:( T:Type, f:(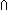 D:Type. D D:Type. D  T). f(f) T). f(f)  T T
Thm*  f:( f:(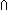 D:Type. D D:Type. D  T), A:Type, a:A, B:Type, b:B. f(a) = f(b) T), A:Type, a:A, B:Type, b:B. f(a) = f(b)  T T
Thm*  f:( f:(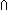 C,D:Type. C C,D:Type. C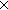 D D  D D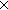 C), A,B:Type, a:A, b:B. f(<a,b>) = <b,a> C), A,B:Type, a:A, b:B. f(<a,b>) = <b,a>  B B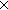 A A
Thm* A 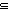 Top Top
|
| Recursive Funs
|
Thm*  x: x: . x! . x!  
Thm* mu  {f:( {f:(   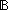 )| )| 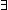 x: x: . f(x) } . f(x) }  
Thm*  A:Type, n: A:Type, n: . (A^n) . (A^n)  Type Type
|
| Recursive Types
|
Thm*  A:Type. Sexpr(A) A:Type. Sexpr(A)  Type Type
Thm*  a,b,c:X. a,b,c:X.
Thm* Reverse(Cons(Inj(a);Cons(Inj(b);Inj(c))))
Thm* =
Thm* Cons(Cons(Inj(c);Inj(b));Inj(a))
|
| Propositions
|
Thm*  A,B:Prop. (A & B) A,B:Prop. (A & B)  Prop Prop
Thm*  A:Type, P:(A A:Type, P:(A  Prop). ( Prop). (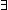 x:A. P(x)) x:A. P(x))  Prop Prop
|
| High-Order Props
|
Thm* A 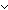 B B 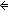  ( ( C:Prop. (A C:Prop. (A   C) C)   (B (B   C) C)   C) C)
|
| Guarded Types
|
Thm*  A:Prop, B:Prop(given A). (A & B) A:Prop, B:Prop(given A). (A & B)  Prop Prop
|
| Type Functionality
|
Thm*  A,B:Type{i}. A+B A,B:Type{i}. A+B  Type{i} Type{i}
Thm* Type{i}  Type{i'} Type{i'}
|
| Prop Levels
|
Thm* Prop{i}  Type{i'} Type{i'}
Thm* Prop{i} 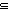 Prop{i'} Prop{i'}
Thm*  A,B:Prop{i}. ( A,B:Prop{i}. ( C:Prop{i}. (A C:Prop{i}. (A   C) C)   (B (B   C) C)   C) C)  Prop{i'} Prop{i'}
|
| Type Conclusions
|
Thm* x:( List) List)  {y: {y: | y greater-bounds x } | y greater-bounds x }
|
| Restricted Decls
|
Thm* 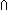 k: k: . x:( . x:( k List) k List)  {y: {y: (k+1)| y greater-bounds x } (k+1)| y greater-bounds x }
|
| Extraction
|
Thm* ext{sfa_doc_find_intlist_great_bound}
Thm*  x:( x:( List) List)  {y: {y: | y greater-bounds x } | y greater-bounds x }
|
| Props as Types
|
Thm* P 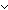 Q Q   ( (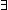 x: x: . (x = 0 . (x = 0   P) & (x P) & (x 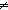 0 0   Q)) Q))
Thm* Dec(P) 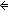  ( (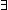 b: b: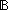 . P . P 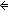  b) b)
|
| Prop Witnesses
|
Thm*  x: x: . . 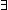 y: y: . y . y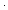 y y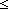 x & x<(y+1) x & x<(y+1)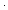 (y+1) (y+1)
|