| 2 | 3. k: 
4. c:  n n   k k
5. p:  k k  ( ( List) List)
6. sum(||p(j)|| | j < k) = n-1
7.  j: j: k, x,y: k, x,y: ||p(j)||. x < y ||p(j)||. x < y   (p(j))[x] > (p(j))[y] (p(j))[x] > (p(j))[y]
8.  j: j: k, x: k, x: ||p(j)||. (p(j))[x] < n-1 & c((p(j))[x]) = j ||p(j)||. (p(j))[x] < n-1 & c((p(j))[x]) = j
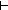 ( ( j: j: k, x,y: k, x,y: ||if c(n-1)= ||if c(n-1)=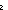 j j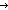 [(n-1) / (p(j))] else p(j) fi||. x < y [(n-1) / (p(j))] else p(j) fi||. x < y   if c(n-1)= if c(n-1)=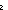 j j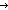 [(n-1) / (p(j))] else p(j) fi[x] > if c(n-1)= [(n-1) / (p(j))] else p(j) fi[x] > if c(n-1)=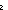 j j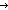 [(n-1) / (p(j))] else p(j) fi[y]) & ( [(n-1) / (p(j))] else p(j) fi[y]) & ( j: j: k, x: k, x: ||if c(n-1)= ||if c(n-1)=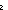 j j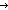 [(n-1) / (p(j))] else p(j) fi||. if c(n-1)= [(n-1) / (p(j))] else p(j) fi||. if c(n-1)=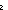 j j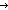 [(n-1) / (p(j))] else p(j) fi[x] < n & c(if c(n-1)= [(n-1) / (p(j))] else p(j) fi[x] < n & c(if c(n-1)=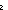 j j [(n-1) / (p(j))] else p(j) fi[x]) = j) [(n-1) / (p(j))] else p(j) fi[x]) = j) | 14 steps |