Thm*  the_es:ES, e',e:E. Dec((e <loc e')) the_es:ES, e',e:E. Dec((e <loc e')) | [decidable__es-locl] |
Thm*  the_es:ES, e,e':E. the_es:ES, e,e':E.
Thm* (e <loc e')    first(e') & e = pred(e') first(e') & e = pred(e')  E E 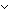 (e <loc pred(e')) (e <loc pred(e')) | [es-locl-iff] |
Thm*  es:ES, e,e':E. e es:ES, e,e':E. e 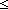 e' e'   loc(e) = loc(e') loc(e) = loc(e')  Id Id | [es-le-loc] |
Thm*  es:ES, e:E, l:IdLnk, tg:Id. es:ES, e:E, l:IdLnk, tg:Id.
Thm* kind(e) = rcv(l; tg)
Thm*  
Thm* loc(e) = destination(l) & loc(sender(e)) = source(l) | [es-loc-rcv] |
Thm*  the_es:ES, e:E. the_es:ES, e:E.  first(e) first(e)   loc(pred(e)) = loc(e) loc(pred(e)) = loc(e)  Id Id | [es-loc-pred] |
Thm*  the_es:ES, j,e:E. first(j) the_es:ES, j,e:E. first(j)    (e <loc j) (e <loc j) | [es-first-implies] |
Thm*  the_es:ES, j:E. the_es:ES, j:E.  first(j) first(j)   (pred(j) <loc j) (pred(j) <loc j) | [es-pred-locl] |
Thm*  the_es:ES, e:E. the_es:ES, e:E.  (e <loc e) (e <loc e) | [es-locl-antireflexive] |
Thm*  the_es:ES. SWellFounded((x <loc y)) the_es:ES. SWellFounded((x <loc y)) | [es-locl-swellfnd] |
Thm*  the_es:ES. Trans x,y:E. x the_es:ES. Trans x,y:E. x 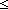 y y | [es-le-trans] |
Thm*  the_es:ES. Trans x,y:E. (x <loc y) the_es:ES. Trans x,y:E. (x <loc y) | [es-locl-trans] |
Thm*  the_es:ES. WellFnd{i}(E;x,y.(x <loc y)) the_es:ES. WellFnd{i}(E;x,y.(x <loc y)) | [es-locl-wellfnd] |
Thm*  the_es:ES. the_es:ES.
Thm* (Trans e,e':E. (e <loc e'))
Thm* & SWellFounded((e <loc e'))
Thm* & ( e,e':E. loc(e) = loc(e') e,e':E. loc(e) = loc(e')  Id Id   (e <loc e') (e <loc e') 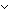 e = e' e = e' 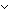 (e' <loc e)) (e' <loc e))
Thm* & ( e:E. first(e) e:E. first(e)   ( ( e':E. e':E.  (e' <loc e))) (e' <loc e)))
Thm* & ( e:E. e:E.
Thm* & ( first(e) first(e)
Thm* & ( 
Thm* & ((pred(e) <loc e) & ( e':E. e':E.  ((pred(e) <loc e') & (e' <loc e)))) ((pred(e) <loc e') & (e' <loc e))))
Thm* & ( e:E. e:E.
Thm* & ( first(e) first(e)
Thm* & ( 
Thm* & (( x:Id. (x when e) = (x after pred(e)) x:Id. (x when e) = (x after pred(e))  vartype(loc(e);x))) vartype(loc(e);x)))
Thm* & (Trans e,e':E. (e < e'))
Thm* & SWellFounded((e < e'))
Thm* & ( e:E. e:E.
Thm* & (isrcv(e)
Thm* & ( 
Thm* & (sends(lnk(e);sender(e))[index(e)] = msg(lnk(e);tag(e);val(e))  Msg) Msg)
Thm* & ( e,e':E. (e <loc e') e,e':E. (e <loc e')   (e < e')) (e < e'))
Thm* & ( e:E. isrcv(e) e:E. isrcv(e)   (sender(e) < e)) (sender(e) < e))
Thm* & ( e,e':E. e,e':E.
Thm* & ((e < e')
Thm* & ( 
Thm* & ( first(e') & (e < pred(e')) first(e') & (e < pred(e')) 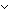 e = pred(e') e = pred(e')  E E
Thm* & (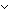 isrcv(e') & (e < sender(e')) isrcv(e') & (e < sender(e')) 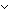 e = sender(e') e = sender(e')  E) E)
Thm* & ( e:E. isrcv(e) e:E. isrcv(e)   loc(e) = destination(lnk(e))) loc(e) = destination(lnk(e)))
Thm* & ( e:E, l:IdLnk. e:E, l:IdLnk.
Thm* & ( loc(e) = source(l) loc(e) = source(l)   sends(l;e) = nil sends(l;e) = nil  (Msg on l) List) (Msg on l) List)
Thm* & ( e,e':E. e,e':E.
Thm* & (isrcv(e)
Thm* & ( 
Thm* & (isrcv(e')
Thm* & ( 
Thm* & (lnk(e) = lnk(e')
Thm* & ( 
Thm* & (((e <loc e')
Thm* & (( 
Thm* & (((sender(e) <loc sender(e'))
Thm* & ((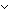 sender(e) = sender(e') sender(e) = sender(e')  E & index(e)<index(e'))) E & index(e)<index(e')))
Thm* & ( e:E, l:IdLnk, n: e:E, l:IdLnk, n: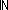 ||sends(l;e)||. ||sends(l;e)||.
Thm* & (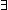 e':E. isrcv(e') & lnk(e') = l & sender(e') = e e':E. isrcv(e') & lnk(e') = l & sender(e') = e  E & index(e') = n E & index(e') = n  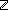 ) ) | [es-axioms] |
Thm*  the_es:ES, e,e':E. (e < e') the_es:ES, e,e':E. (e < e')  Prop Prop | [es-causl_wf] |
Thm*  the_es:ES, e:E. the_es:ES, e:E.  first(e) first(e)   pred(e) pred(e)  E E | [es-pred_wf] |
Thm*  the_es:ES, e:E. first(e) the_es:ES, e:E. first(e)  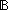 | [es-first_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)   index(e) index(e)  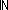 ||sends(lnk(e);sender(e))|| ||sends(lnk(e);sender(e))|| | [es-index_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)   sender(e) sender(e)  E E | [es-sender_wf] |
Thm*  the_es:ES, l:IdLnk, e:E. sends(l;e) the_es:ES, l:IdLnk, e:E. sends(l;e)  (Msg on l) List (Msg on l) List | [es-sends_wf] |
Thm*  the_es:ES, e:E, x:Id. (x after e) the_es:ES, e:E, x:Id. (x after e)  vartype(loc(e);x) vartype(loc(e);x) | [es-after_wf] |
Thm*  the_es:ES, e:E, x:Id. (x when e) the_es:ES, e:E, x:Id. (x when e)  vartype(loc(e);x) vartype(loc(e);x) | [es-when_wf] |
Thm*  the_es:ES, e:E. val(e) the_es:ES, e:E. val(e)  valtype(e) valtype(e) | [es-val_wf] |
Thm*  the_es:ES, i,x:Id. vartype(i;x) the_es:ES, i,x:Id. vartype(i;x)  Type Type | [es-vartype_wf] |
Thm*  the_es:ES, e:E. valtype(e) the_es:ES, e:E. valtype(e)  Type Type | [es-valtype_wf] |
Thm*  the_es:ES, e:E. the_es:ES, e:E.  isrcv(e) isrcv(e)   acttype(e) acttype(e)  Type Type | [es-acttype_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)   rcvtype(e) rcvtype(e)  Type Type | [es-rcvtype_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)   lnk(e) lnk(e)  IdLnk IdLnk | [es-lnk_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)   tag(e) tag(e)  Id Id | [es-tag_wf] |
Thm*  the_es:ES, e:E. isrcv(e) the_es:ES, e:E. isrcv(e)  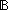 | [es-isrcv_wf] |
Thm*  the_es:ES, e:E. kind(e) the_es:ES, e:E. kind(e)  Knd Knd | [es-kind_wf] |
Thm*  the_es:ES, e:E. loc(e) the_es:ES, e:E. loc(e)  Id Id | [es-loc_wf] |
Thm*  the_es:ES, l:IdLnk. (Msg on l) the_es:ES, l:IdLnk. (Msg on l)  Type Type | [es-Msgl_wf] |
Thm*  the_es:ES. Msg the_es:ES. Msg  Type Type | [es-Msg_wf] |
Thm*  the_es:ES, e,e':E. Dec(e = e') the_es:ES, e,e':E. Dec(e = e') | [decidable__es-E_equal] |
Thm*  the_es:ES, e,e':E. e = e' the_es:ES, e,e':E. e = e'   e = e' e = e' | [assert-es-eq-E] |
Thm*  the_es:ES, e,e':E. e = e' the_es:ES, e,e':E. e = e'  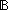 | [es-eq-E_wf] |
Thm*  the_es:ES. E the_es:ES. E  Type Type | [es-E_wf] |
Thm*  E:Type, eq:EqDecider(E), T,V:(Id E:Type, eq:EqDecider(E), T,V:(Id  Id Id  Type), M:(IdLnk Type), M:(IdLnk  Id Id  Type), Type),
Thm*  loc:(E loc:(E  Id), k:(E Id), k:(E  Knd), v:(e:E Knd), v:(e:E  eventtype(k;loc;V;M;e)), eventtype(k;loc;V;M;e)),
Thm*  w,a:(x:Id w,a:(x:Id  e:E e:E  T(loc(e),x)), snds:(l:IdLnk T(loc(e),x)), snds:(l:IdLnk  E E  (Msg_sub(l; M) List)), (Msg_sub(l; M) List)),
Thm*  sndr:({e:E| isrcv(k(e)) } sndr:({e:E| isrcv(k(e)) }  E), i:(e:{e:E| isrcv(k(e)) } E), i:(e:{e:E| isrcv(k(e)) }  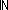 ||snds ||snds
Thm*  sndr:({e:E| isrcv(k(e)) } sndr:({e:E| isrcv(k(e)) }  E), i:(e:{e:E| isrcv(k(e)) } E), i:(e:{e:E| isrcv(k(e)) }   ||(lnk(k(e)) ||(lnk(k(e))
Thm*  sndr:({e:E| isrcv(k(e)) } sndr:({e:E| isrcv(k(e)) }  E), i:(e:{e:E| isrcv(k(e)) } E), i:(e:{e:E| isrcv(k(e)) }   ||,sndr(e))||), ||,sndr(e))||),
Thm*  f:(E f:(E  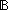 ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms{i:l} Prop), p:ESAxioms{i:l}
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(E; Prop), p:ESAxioms(E;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(T; Prop), p:ESAxioms(T;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(M; Prop), p:ESAxioms(M;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(loc; Prop), p:ESAxioms(loc;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(k; Prop), p:ESAxioms(k;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(v; Prop), p:ESAxioms(v;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(w; Prop), p:ESAxioms(w;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(a; Prop), p:ESAxioms(a;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(snds; Prop), p:ESAxioms(snds;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(sndr; Prop), p:ESAxioms(sndr;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(i; Prop), p:ESAxioms(i;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(f; Prop), p:ESAxioms(f;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(prd; Prop), p:ESAxioms(prd;
Thm*  f:(E f:(E   ), prd:({e':E| ), prd:({e':E|  f(e') } f(e') }  E), cl:(E E), cl:(E  E E  Prop), p:ESAxioms(cl). Prop), p:ESAxioms(cl).
Thm* mk-es(E; eq; T; V; M; loc; k; v; w; a; snds; sndr; i; f; prd; cl; p)  ES ES | [mk-es_wf] |
Thm*  E:Type{i}, T,V:(Id E:Type{i}, T,V:(Id  Id Id  Type{i}), M:(IdLnk Type{i}), M:(IdLnk  Id Id  Type{i}), loc:(E Type{i}), loc:(E  Id), Id),
Thm*  kind:(E kind:(E  Knd), val:(e:E Knd), val:(e:E  eventtype(kind;loc;V;M;e)), eventtype(kind;loc;V;M;e)),
Thm*  when,after:(x:Id when,after:(x:Id  e:E e:E  T(loc(e),x)), T(loc(e),x)),
Thm*  sends:(l:IdLnk sends:(l:IdLnk  E E  (Msg_sub(l; M) List)), (Msg_sub(l; M) List)),
Thm*  sender:({e:E| isrcv(kind(e)) } sender:({e:E| isrcv(kind(e)) }  E), E),
Thm*  index:(e:{e:E| isrcv(kind(e)) } index:(e:{e:E| isrcv(kind(e)) }  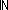 ||sends(lnk(kind(e)),sender(e))||), ||sends(lnk(kind(e)),sender(e))||),
Thm*  first:(E first:(E  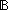 ), pred:({e':E| ), pred:({e':E|  first(e') } first(e') }  E), causl:(E E), causl:(E  E E  Prop{i}). Prop{i}).
Thm* ESAxioms{i:l}
Thm* ESAxioms(E;
Thm* ESAxioms(T;
Thm* ESAxioms(M;
Thm* ESAxioms(loc;
Thm* ESAxioms(kind;
Thm* ESAxioms(val;
Thm* ESAxioms(when;
Thm* ESAxioms(after;
Thm* ESAxioms(sends;
Thm* ESAxioms(sender;
Thm* ESAxioms(index;
Thm* ESAxioms(first;
Thm* ESAxioms(pred;
Thm* ESAxioms(causl)
Thm*  Prop{i'} Prop{i'} | [ESAxioms_wf] |
Thm*  E:Type, V:(Id E:Type, V:(Id  Id Id  Type), M:(IdLnk Type), M:(IdLnk  Id Id  Type), loc:(E Type), loc:(E  Id), k:(E Id), k:(E  Knd), Knd),
Thm*  e:E. eventtype(k;loc;V;M;e) e:E. eventtype(k;loc;V;M;e)  Type Type | [eventtype_wf] |
Thm*  R:(T R:(T  T T  Prop), x,y:T. (x R^+ y) Prop), x,y:T. (x R^+ y)   (x R y) (x R y) 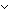 ( (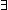 z:T. (x R^+ z) & (z R y)) z:T. (x R^+ z) & (z R y)) | [rel_plus_implies] |
Thm*  R:(T R:(T  T T  Prop). Trans x,y:T. x R^+ y Prop). Trans x,y:T. x R^+ y | [rel_plus_trans] |
Thm*  R:(T R:(T  T T  Type). SWellFounded(R(x,y)) Type). SWellFounded(R(x,y))   WellFnd{i}(T;x,y.R(x,y)) WellFnd{i}(T;x,y.R(x,y)) | [strongwf-implies] |
Thm*  i:Id, k:Knd. has-src(i;k) i:Id, k:Knd. has-src(i;k)   isrcv(k) & source(lnk(k)) = i isrcv(k) & source(lnk(k)) = i | [assert-has-src] |
Thm*  i:Id, k:Knd. has-src(i;k) i:Id, k:Knd. has-src(i;k)  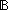 | [has-src_wf] |
Thm*  a,b:Knd. a = b a,b:Knd. a = b   a = b a = b | [assert-eq-knd] |
Thm*  p:IdLnk List, i: p:IdLnk List, i: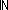 ||p||, j: ||p||, j: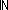 (i+1). (i+1).
Thm* lpath(p)   lconnects(l_interval(p;j;i);source(p[j]);source(p[i])) lconnects(l_interval(p;j;i);source(p[j]);source(p[i])) | [lpath-members-connected] |
Thm*  p:IdLnk List, i,j:Id. lconnects(p;i;j) p:IdLnk List, i,j:Id. lconnects(p;i;j)  Prop Prop | [lconnects_wf] |
Thm*  l:IdLnk, p:IdLnk List. l:IdLnk, p:IdLnk List.
Thm* lpath([l / p])
Thm*  
Thm* lpath(p)
Thm* & ( ||p|| = 0 ||p|| = 0  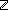   destination(l) = source(hd(p)) & destination(l) = source(hd(p)) &  hd(p) = lnk-inv(l)) hd(p) = lnk-inv(l)) | [lpath_cons] |
Thm*  l:IdLnk. destination(lnk-inv(l)) = source(l) l:IdLnk. destination(lnk-inv(l)) = source(l) | [ldst-inv] |
Thm*  l:IdLnk. source(lnk-inv(l)) = destination(l) l:IdLnk. source(lnk-inv(l)) = destination(l) | [lsrc-inv] |
Thm*  x:A. ( x:A. ( x,y:A. Dec(x = y)) x,y:A. Dec(x = y))   ( ( L:A List. Dec((x L:A List. Dec((x  L))) L))) | [decidable__l_member] |
Thm*  a,b:IdLnk. Dec(a = b) a,b:IdLnk. Dec(a = b) | [decidable__equal_IdLnk] |
Thm*  a,b:IdLnk. a = b a,b:IdLnk. a = b   a = b a = b | [assert-eq-lnk] |
Thm*  a,b:Id. Dec(a = b) a,b:Id. Dec(a = b) | [decidable__equal_Id] |
Thm*  a,b:Id. a = b a,b:Id. a = b   a = b a = b | [assert-eq-id] |
Thm*  a:Id. a = a ~ true a:Id. a = a ~ true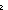 | [eq_id_self] |
Thm*  eq:EqDecider(A), L:A List, x:A. deq-member(eq;x;L) eq:EqDecider(A), L:A List, x:A. deq-member(eq;x;L)   (x (x  L) L) | [assert-deq-member] |
Thm*  A,B:Type, a:EqDecider(A), b:EqDecider(B). A,B:Type, a:EqDecider(A), b:EqDecider(B).
Thm* sum-deq(A;B;a;b)  ( ( p,q:A+B. p = q p,q:A+B. p = q   sumdeq(a;b)(p,q)) sumdeq(a;b)(p,q)) | [sum-deq_wf] |
Thm*  a:EqDecider(A), b:EqDecider(B), p,q:A+B. p = q a:EqDecider(A), b:EqDecider(B), p,q:A+B. p = q   sumdeq(a;b)(p,q) sumdeq(a;b)(p,q) | [sumdeq-property] |
Thm*  A,B:Type, a:EqDecider(A), b:EqDecider(B). A,B:Type, a:EqDecider(A), b:EqDecider(B).
Thm* prod-deq(A;B;a;b)  ( ( p,q:(A p,q:(A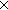 B). p = q B). p = q   proddeq(a;b)(p,q)) proddeq(a;b)(p,q)) | [prod-deq_wf] |
Thm*  a:EqDecider(A), b:EqDecider(B), p,q:(A a:EqDecider(A), b:EqDecider(B), p,q:(A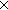 B). p = q B). p = q   proddeq(a;b)(p,q) proddeq(a;b)(p,q) | [proddeq-property] |
Thm*  a,b:Atom. a = b a,b:Atom. a = b   a= a=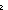 b b Atom Atom | [atom-deq-aux] |
Thm*  a,b: a,b: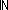 . a = b . a = b   a= a=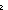 b b | [nat-deq-aux] |
Thm* strong-subtype(A;B)   (EqDecider(B) (EqDecider(B) 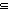 r EqDecider(A)) r EqDecider(A)) | [strong-subtype-deq-subtype] |
Thm*  d:EqDecider(B). strong-subtype(A;B) d:EqDecider(B). strong-subtype(A;B)   d d  EqDecider(A) EqDecider(A) | [strong-subtype-deq] |
Thm*  d:EqDecider(A), i:A. (eqof(d)(i,i)) ~ true d:EqDecider(A), i:A. (eqof(d)(i,i)) ~ true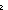 | [eqof_eq_btrue] |
Thm*  d:EqDecider(T), x,y:T. x = y d:EqDecider(T), x,y:T. x = y   eqof(d)(x,y) eqof(d)(x,y) | [deq_property] |
Thm*  B:Type, k:Knd, f:(Id B:Type, k:Knd, f:(Id  B), g:(IdLnk B), g:(IdLnk  Id Id  B). B).
Thm* kindcase(k;a.f(a);l,t.g(l,t))  B B | [kindcase_wf] |
Def ESAxioms{i:l}
Def ESAxioms(E;
Def ESAxioms(T;
Def ESAxioms(M;
Def ESAxioms(loc;
Def ESAxioms(kind;
Def ESAxioms(val;
Def ESAxioms(when;
Def ESAxioms(after;
Def ESAxioms(sends;
Def ESAxioms(sender;
Def ESAxioms(index;
Def ESAxioms(first;
Def ESAxioms(pred;
Def ESAxioms(causl)
Def == ( e,e':E. loc(e) = loc(e') e,e':E. loc(e) = loc(e')  Id Id   causl(e,e') causl(e,e') 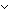 e = e' e = e' 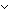 causl(e',e)) causl(e',e))
Def == & ( e:E. e:E.  (first(e)) (first(e))   ( ( e':E. loc(e') = loc(e) e':E. loc(e') = loc(e)  Id Id    causl(e',e))) causl(e',e)))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))
Def == & ( 
Def == & (loc(pred(e)) = loc(e)  Id & causl(pred(e),e) Id & causl(pred(e),e)
Def == & (& ( e':E. e':E.
Def == & (& (loc(e') = loc(e)  Id Id    (causl(pred(e),e') & causl(e',e)))) (causl(pred(e),e') & causl(e',e))))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))   ( ( x:Id. when(x,e) = after(x,pred(e)) x:Id. when(x,e) = after(x,pred(e))  T(loc(e),x))) T(loc(e),x)))
Def == & (Trans e,e':E. causl(e,e'))
Def == & SWellFounded(causl(e,e'))
Def == & ( e:E. e:E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ((sends(lnk(kind(e)),sender(e)))[(index(e))]
Def == & (=
Def == & (msg(lnk(kind(e));tag(kind(e));val(e))
Def == & ( Msg(M)) Msg(M))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   causl(sender(e),e)) causl(sender(e),e))
Def == & ( e,e':E. e,e':E.
Def == & (causl(e,e')
Def == & ( 
Def == & (  (first(e')) & causl(e,pred(e')) (first(e')) & causl(e,pred(e')) 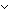 e = pred(e') e = pred(e')
Def == & (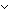  isrcv(kind(e')) & causl(e,sender(e')) isrcv(kind(e')) & causl(e,sender(e')) 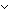 e = sender(e')) e = sender(e'))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   loc(e) = destination(lnk(kind(e)))) loc(e) = destination(lnk(kind(e))))
Def == & ( e:E, l:IdLnk. e:E, l:IdLnk.
Def == & ( loc(e) = source(l) loc(e) = source(l)   sends(l,e) = nil sends(l,e) = nil  Msg_sub(l; M) List) Msg_sub(l; M) List)
Def == & ( e,e':E. e,e':E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ( isrcv(kind(e')) isrcv(kind(e'))
Def == & ( 
Def == & (lnk(kind(e)) = lnk(kind(e'))
Def == & ( 
Def == & ((causl(e,e')
Def == & (( 
Def == & ((causl(sender(e),sender(e'))
Def == & ((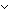 sender(e) = sender(e') sender(e) = sender(e')  E & index(e)<index(e'))) E & index(e)<index(e')))
Def == & ( e:E, l:IdLnk, n: e:E, l:IdLnk, n: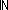 ||sends(l,e)||. ||sends(l,e)||.
Def == & (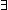 e':E. e':E.
Def == & ( isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) | [ESAxioms] |
Def SWellFounded(R(x;y)) == 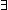 f:(T f:(T  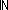 ). ).  x,y:T. R(x;y) x,y:T. R(x;y)   f(x)<f(y) f(x)<f(y) | [strongwellfounded] |
Def lpath(p)
Def ==  i: i: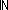 (||p||-1). (||p||-1).
Def == destination(p[i]) = source(p[(i+1)]) &  p[(i+1)] = lnk-inv(p[i]) p[(i+1)] = lnk-inv(p[i])  IdLnk IdLnk | [lpath] |
Def EqDecider(T) == eq:T  T T  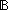 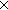  x,y:T. x = y x,y:T. x = y    (eq(x,y)) (eq(x,y)) | [deq] |