{ 
s:SES
(SecurityAxioms
(es:EO+(Info). A:Id. thr:Thread.
(Legal(thr)@A
(n:E(New). e:Act.
(e 
thr
e has* New(n)
(
e':E
((e' <loc e) 
Action(e') e' has* New(n) e' thr))
(e = n)
supposing e':E
((e' < e)
Action(e')
e' has* New(n)
((loc(e') = A) (
e' 
Send)))))))) }
{ Proof }
Definitions occuring in Statement :
ses-legal-thread: Legal(thr)@A,
ses-thread-member: e thr,
ses-thread: Thread,
ses-axioms: SecurityAxioms,
event-has*: e has* a,
ses-act: Act,
ses-action: Action(e),
ses-send: Send,
ses-new: New,
ses-info: Info,
security-event-structure: SES,
es-E-interface: E(X),
eclass-val: X(e),
in-eclass: e X,
event-ordering+: EO+(Info),
es-locl: (e <loc e'),
es-causl: (e < e'),
es-loc: loc(e),
es-E: E,
Id: Id,
assert: b,
uimplies: b supposing a,
all: x:A. B[x],
exists: x:A. B[x],
not: A,
implies: P Q,
or: P Q,
and: P Q,
equal: s = t
Definitions :
all: x:A. B[x],
implies: P Q,
ses-act: Act,
uimplies: b supposing a,
and: P Q,
not: A,
assert: b,
or: P Q,
exists: x:A. B[x],
prop: 
,
member: t T,
squash: 
T,
true: True,
false: False,
top: Top,
so_lambda: 
x y.t[x; y],
btrue: tt,
guard: {T},
ifthenelse: if b then t else f fi ,
cand: A c B,
nat: 
,
infix_ap: x f y,
ge: i 
j ,
le: A 
B,
es-E-interface: E(X),
ses-action: Action(e),
ses-used-atoms: UsedAtoms(e),
bfalse: ff,
ses-info-flow: ->>,
event-has*: e has* a,
rel_star: R^*,
event-has: (e has a),
class-value-has: X(e) has a,
rel_exp: R^n,
ycomb: Y,
eq_int: (i =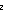
j),
so_apply: x[s1;s2],
same-action: same-action(x;y),
nat_plus: 
,
es-le: e loc e' ,
sq_stable: SqStable(P),
uall: [x:A]. B[x],
decidable: Dec(P),
sq_type: SQType(T),
strongwellfounded: SWellFounded(R[x; y]),
ses-axioms: SecurityAxioms,
rev_implies: P 
Q,
iff: P Q,
ses-R: PropertyR,
bool: 
,
unit: Unit,
ses-D: PropertyD,
es-locl: (e <loc e'),
ses-NU: PropertyNU,
ses-disjoint: ActionsDisjoint,
ses-nonce-disjoint: NoncesCiphersAndKeysDisjoint,
ses-flow-axiom: PropertyF,
ses-V: PropertyV,
ses-S: PropertyS,
ses-K: PropertyK,
subtype: S 
T,
it: 
,
!hyp_hide: x
Lemmas :
sq_stable_from_decidable,
ses-action_wf,
decidable__ses-action,
assert_wf,
in-eclass_wf,
ses-info_wf,
ses-send_wf,
es-interface-subtype_rel2,
sdata_wf,
es-E_wf,
event-ordering+_inc,
event-ordering+_wf,
top_wf,
event-has*_wf,
eclass-val_wf,
ses-new_wf,
subtype_base_sq,
bool_subtype_base,
es-causl_wf,
decidable__es-E-equal,
es-locl_wf,
bool_wf,
ses-thread-member_wf,
Id_wf,
es-loc_wf,
not_wf,
ses-act_wf,
es-E-interface_wf,
ses-legal-thread_wf,
ses-thread_wf,
ses-axioms_wf,
security-event-structure_wf,
assert_elim,
es-causl-swellfnd,
nat_properties,
ge_wf,
nat_wf,
le_wf,
es-le_wf,
event-has_wf,
rel_exp_wf,
ses-info-flow_wf,
ses-legal-thread-has-atom,
event-has*-iff,
member-useable-atoms,
ses-rcv_wf,
es-causle_weakening_locl,
es-causl_transitivity2,
ses-encrypt_wf,
encryption-key_wf,
ses-decrypt_wf,
ses-sign_wf,
ses-verify_wf,
ses-act-has-atom,
decidable__l_member,
decidable__atom_equal_1,
ses-useable-atoms_wf,
l_member_wf,
ses-used-atoms_wf,
iff_weakening_uiff,
eqtt_to_assert,
uiff_transitivity,
bnot_wf,
eqff_to_assert,
assert_of_bnot,
sdata-atoms_wf,
squash_wf,
true_wf,
ses-legal-thread-decrypt,
atom1_subtype_base,
sdata_subtype_base,
member-used-atoms,
encryption-key-atoms_wf,
ses-encryption-key_wf,
ses-signed_wf,
ses-verify-sig_wf,
ses-verify-signed_wf,
ses-cipher_wf,
ses-decryption-key_wf,
decidable__es-le,
es-locl_transitivity2,
es-le_weakening,
ses-sig_wf,
ses-crypt_wf,
ses-decrypted_wf,
ses-nonce-unique,
ses-nonce-from-ordering,
ses-flow-axiom-ordering,
rel_exp_iff,
rel_star_wf,
class-value-has_wf,
free-from-atom_wf1,
event-has*-transitive-encrypt,
ses-cipher-unique,
decidable__equal_int,
int_subtype_base,
event-has_functionality,
eclass_wf,
ses-info-flow-exp_functionality
\mforall{}s:SES
(SecurityAxioms
{}\mRightarrow{} (\mforall{}es:EO+(Info). \mforall{}A:Id. \mforall{}thr:Thread.
(Legal(thr)@A
{}\mRightarrow{} (\mforall{}n:E(New). \mforall{}e:Act.
(e \mmember{} thr
{}\mRightarrow{} e has* New(n)
{}\mRightarrow{} (\mexists{}e':E. ((e' <loc e) \mwedge{} Action(e') \mwedge{} e' has* New(n) \mwedge{} e' \mmember{} thr)) \mvee{} (e = n)
supposing \mforall{}e':E
((e' < e)
{}\mRightarrow{} Action(e')
{}\mRightarrow{} e' has* New(n)
{}\mRightarrow{} ((loc(e') = A) \mwedge{} (\mneg{}\muparrow{}e' \mmember{}\msubb{} Send))))))))
Date html generated:
2011_08_17-PM-07_36_33
Last ObjectModification:
2011_06_18-PM-01_28_51
Home
Index