{ 
[n:
]. (str-to-nat(nat-to-str(n)) = n) }
{ Proof }
Definitions occuring in Statement :
str-to-nat: str-to-nat(s),
nat-to-str: nat-to-str(n),
nat: ,
uall: [x:A]. B[x],
int: 
,
equal: s = t
Definitions :
uall: [x:A]. B[x],
nat: ,
str-to-nat: str-to-nat(s),
nat-to-str: nat-to-str(n),
all: x:A. B[x],
implies: P 
Q,
ge: i 
j ,
member: t 
T,
le: A 
B,
not: 
A,
false: False,
prop: 
,
ycomb: Y,
ifthenelse: if b then t else f fi ,
btrue: tt,
str-to-nat-plus: str-to-nat-plus(s;n),
str1-to-nat: str1-to-nat(a),
eq_atom: x =a y,
bfalse: ff,
int_nzero: 
,
nequal: a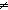 
b T ,
nat_plus: 
,
and: P 
Q,
length: ||as||,
append: as @ bs,
top: Top,
subtype: S 
T,
rev_implies: P 
Q,
iff: P Q,
so_lambda: 
x.t[x],
label: ...$L... t,
bool: 
,
unit: Unit,
sq_type: SQType(T),
uimplies: b supposing a,
guard: {T},
so_apply: x[s],
it: 
Lemmas :
nat_properties,
ge_wf,
str-to-nat_wf,
nat-to-str_wf,
le_wf,
nat_wf,
eq_int_wf,
bool_wf,
iff_weakening_uiff,
uiff_transitivity,
assert_wf,
eqtt_to_assert,
assert_of_eq_int,
not_wf,
bnot_wf,
eqff_to_assert,
assert_of_bnot,
not_functionality_wrt_uiff,
div_rem_sum,
nequal_wf,
rem_bounds_1,
divide_wf,
append_wf,
length_wf1,
remainder_wf,
subtype_base_sq,
int_subtype_base,
str-to-nat-plus_wf,
str1-to-nat_wf,
non_neg_length,
length_wf_nat,
top_wf,
exp_wf2,
str-to-nat-plus-property,
add_functionality_wrt_eq,
exp_wf,
set_subtype_base,
length_nil,
length_cons,
length_append,
exp_add,
exp1
\mforall{}[n:\mBbbN{}]. (str-to-nat(nat-to-str(n)) = n)
Date html generated:
2011_08_10-AM-07_42_48
Last ObjectModification:
2011_06_18-AM-08_09_45
Home
Index