At: switch inv rel closure lemma1 1 1 2 1 1 2 1 1
1. E: EventStruct
2. tr: |E| List
3. ls:  ||tr||
||tr||
4. is-send(E)(tr[ls])
5.  j:
j: ||tr||. ls < j
||tr||. ls < j 

 is-send(E)(tr[j])
is-send(E)(tr[j])
6. n: 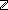
7. 0 < n
8.  i,j:
i,j: ||tr||.
i
||tr||.
i j
j 
 is-send(E)(tr[i])
is-send(E)(tr[i]) 
 is-send(E)(tr[j])
is-send(E)(tr[j]) 
 (i switchR(tr)^n-1 ls)
(i switchR(tr)^n-1 ls) 
 (j (switchR(tr)^*) ls)
(j (switchR(tr)^*) ls)
9. i:  ||tr||
||tr||
10. j:  ||tr||
||tr||
11. i j
j
12. is-send(E)(tr[i])
13. is-send(E)(tr[j])
14. i switchR(tr)^n ls
15.  n = 0
n = 0
16. z:  ||tr||
||tr||
17. is-send(E)(tr[i])
18. is-send(E)(tr[z])
19. i < z
20. tr[z] somewhere delivered before tr[i]
21. z switchR(tr)^n-1 ls
22. i (switchR(tr)^*) ls
23. z (switchR(tr)^*) ls
24.  z
z j
j
25. j = i
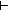 j (switchR(tr)^*) ls
j (switchR(tr)^*) ls
By: HypSubstSq -1 0
Generated subgoals:None
About: