At: nd ext valcom 1 1 2 1 1 1 1 1 1 1 1 5 1 1 1 1 2 2 1 1 1 2 2
1. Alph: Type
2. St: Type
3. NDA: NDA(Alph;St)
4. C: (St Alph*)*
Alph*)*
5. ||C|| > 0
6.  i:
i: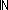 (||C||-1). ||2of(C[i])|| > 0
(||C||-1). ||2of(C[i])|| > 0
7. q: St
8. a: Alph
9. p: St
10. I(NDA) = 1of(hd(C))
11.  i:
i: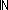 (||C||-1).
(||C||-1).
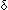 NDA(1of(C[i]),hd(rev(2of(C[i]))),1of(C[(i+1)])) & 2of(C[(i+1)]) = rev(tl(rev(2of(C[i]))))
NDA(1of(C[i]),hd(rev(2of(C[i]))),1of(C[(i+1)])) & 2of(C[(i+1)]) = rev(tl(rev(2of(C[i]))))
12. 1of(hd(rev(C))) = q
13. 2of(hd(rev(C))) = nil
14. 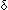 NDA(q,a,p)
NDA(q,a,p)
15. i: 
16. 0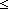 i
i
17. i < ||map( c. < 1of(c),a.2of(c) > ;C)||+1-1
c. < 1of(c),a.2of(c) > ;C)||+1-1
18. i = ||C||-1
19. i+1-||map( c. < 1of(c),a.2of(c) > ;C)|| = 0
c. < 1of(c),a.2of(c) > ;C)|| = 0 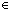
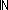 1
1
20. rev(2of(C[i])) = nil
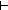
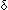 NDA(1of(C[i]),hd([a]),p)
NDA(1of(C[i]),hd([a]),p)
By: Reduce 0
Generated subgoal:| 1 | 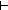 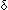 NDA(1of(C[i]),a,p) NDA(1of(C[i]),a,p) |
About: