Nuprl Lemma : bezout_sq_exists_anne
 n,m:
n,m: . (
. (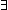 p:{
p:{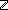
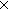
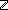 | let x,y = p in GCD(m;n;(x * m) + (y * n))})
| let x,y = p in GCD(m;n;(x * m) + (y * n))})
Proof
Definitions occuring in Statement :
gcd_p: GCD(a;b;y),
nat:  ,
all:
,
all:  x:A. B[x],
sq_exists:
x:A. B[x],
sq_exists: 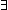 x:{A| B[x]},
spread: spread def,
product: x:A
x:{A| B[x]},
spread: spread def,
product: x:A 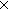 B[x],
multiply: n * m,
add: n + m,
int:
B[x],
multiply: n * m,
add: n + m,
int: 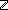
Definitions :
nequal: a 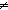 b
b 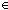 T ,
int_nzero:
T ,
int_nzero: 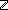

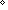 ,
int_seg: {i..j
,
int_seg: {i..j },
lelt: i
},
lelt: i 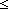 j < k,
and: P
j < k,
and: P 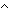 Q,
nat_plus:
Q,
nat_plus: 
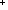 ,
nat:
,
nat:  ,
le: A
,
le: A 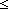 B,
not:
B,
not: 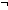 A,
false: False,
all:
A,
false: False,
all:  x:A. B[x],
implies: P
x:A. B[x],
implies: P 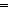
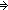 Q,
member: t
Q,
member: t 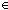 T,
so_lambda:
T,
so_lambda: 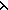
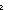 x.t[x],
sq_exists:
x.t[x],
sq_exists: 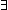 x:{A| B[x]},
so_lambda:
x:{A| B[x]},
so_lambda: 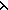
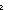 x y.t[x; y],
so_apply: x[s1;s2],
subtype_rel: A
x y.t[x; y],
so_apply: x[s1;s2],
subtype_rel: A 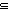 r B,
rev_implies: P
r B,
rev_implies: P 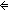
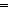 Q,
iff: P
Q,
iff: P 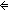
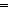
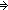 Q,
uimplies: b supposing a,
guard: {T},
sq_type: SQType(T),
decidable: Dec(P),
or: P
Q,
uimplies: b supposing a,
guard: {T},
sq_type: SQType(T),
decidable: Dec(P),
or: P 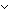 Q,
prop:
Q,
prop: 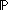 ,
uall:
,
uall:  [x:A]. B[x],
so_apply: x[s]
[x:A]. B[x],
so_apply: x[s]
Lemmas :
div_rem_gcd_anne,
nequal_wf,
int_nzero_properties,
rem_to_div,
rem_bounds_1,
zero-le-nat,
remainder_wf,
lelt_wf,
gcd_p_zero,
subtype_base_sq,
set_subtype_base,
int_subtype_base,
decidable__equal_nat,
le_wf,
all_wf,
int_seg_wf,
nat_wf,
sq_exists_wf,
gcd_p_wf,
natrec_wf
\mforall{}n,m:\mBbbN{}. (\mexists{}p:\{\mBbbZ{} \mtimes{} \mBbbZ{}| let x,y = p in GCD(m;n;(x * m) + (y * n))\})
Date html generated:
2013_09_05-AM-11_16_10
Last ObjectModification:
2013_09_05-AM-10_38_32
Home
Index