Nuprl Lemma : fpf-split
 [A:Type]
[A:Type]
 eq:EqDecider(A)
eq:EqDecider(A)
 [B:A
[B:A 
 Type]
Type]
 f:a:A fp-> B[a]
f:a:A fp-> B[a]
 [P:A
[P:A 

 ]
]
(( a:A. Dec(P[a]))
a:A. Dec(P[a]))

 (
( fp,fnp:a:A fp-> B[a]
fp,fnp:a:A fp-> B[a]
((f  fp
fp 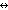 fnp
fnp  fp
fp 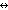 fnp
fnp  f)
f)
 ((
(( a:A. P[a] supposing
a:A. P[a] supposing  a
a  dom(fp))
dom(fp))  (
( a:A.
a:A.  P[a] supposing
P[a] supposing  a
a  dom(fnp)))
dom(fnp)))
 fpf-domain(fp)
fpf-domain(fp)  fpf-domain(f)
fpf-domain(f)
 fpf-domain(fnp)
fpf-domain(fnp)  fpf-domain(f))))
fpf-domain(f))))
Proof not projected
Definitions occuring in Statement :
fpf-join: f 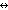 g,
fpf-sub: f
g,
fpf-sub: f  g,
fpf-domain: fpf-domain(f),
fpf-dom: x
g,
fpf-domain: fpf-domain(f),
fpf-dom: x  dom(f),
fpf: a:A fp-> B[a],
assert:
dom(f),
fpf: a:A fp-> B[a],
assert:  b,
decidable: Dec(P),
uimplies: b supposing a,
uall:
b,
decidable: Dec(P),
uimplies: b supposing a,
uall:  [x:A]. B[x],
prop:
[x:A]. B[x],
prop:  ,
so_apply: x[s],
all:
,
so_apply: x[s],
all:  x:A. B[x],
exists:
x:A. B[x],
exists:  x:A. B[x],
not:
x:A. B[x],
not:  A,
implies: P
A,
implies: P 
 Q,
and: P
Q,
and: P  Q,
function: x:A
Q,
function: x:A 
 B[x],
universe: Type,
sublist: L1
B[x],
universe: Type,
sublist: L1  L2,
deq: EqDecider(T)
L2,
deq: EqDecider(T)
Definitions :
uall:  [x:A]. B[x],
all:
[x:A]. B[x],
all:  x:A. B[x],
so_apply: x[s],
prop:
x:A. B[x],
so_apply: x[s],
prop:  ,
implies: P
,
implies: P 
 Q,
member: t
Q,
member: t  T,
so_lambda:
T,
so_lambda: 
 x.t[x],
fpf: a:A fp-> B[a],
false: False,
cand: A c
x.t[x],
fpf: a:A fp-> B[a],
false: False,
cand: A c B,
not:
B,
not:  A,
uimplies: b supposing a,
fpf-sub: f
A,
uimplies: b supposing a,
fpf-sub: f  g,
and: P
g,
and: P  Q,
exists:
Q,
exists:  x:A. B[x],
fpf-cap: f(x)?z,
pi1: fst(t),
fpf-dom: x
x:A. B[x],
fpf-cap: f(x)?z,
pi1: fst(t),
fpf-dom: x  dom(f),
fpf-join: f
dom(f),
fpf-join: f 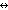 g,
iff: P
g,
iff: P 

 Q,
rev_implies: P
Q,
rev_implies: P 
 Q,
guard: {T},
or: P
Q,
guard: {T},
or: P  Q,
bfalse: ff,
btrue: tt,
ifthenelse: if b then t else f fi ,
fpf-domain: fpf-domain(f),
decidable: Dec(P),
unit: Unit,
bool:
Q,
bfalse: ff,
btrue: tt,
ifthenelse: if b then t else f fi ,
fpf-domain: fpf-domain(f),
decidable: Dec(P),
unit: Unit,
bool:  ,
it:
,
it: 
Lemmas :
all_wf,
decidable_wf,
fpf_wf,
deq_wf,
l_member_wf,
filter_wf,
dcdr-to-bool_wf,
subtype_rel_dep_function,
subtype_rel_sets,
subtype_rel_self,
member_filter,
bnot_wf,
fpf-domain_wf,
sublist_wf,
not_wf,
fpf-sub_wf,
assert_witness,
fpf-trivial-subtype-top,
top_wf,
fpf-join_wf,
fpf-dom_wf,
assert_wf,
pair_wf,
deq-member_wf,
append_wf,
assert-deq-member,
not_functionality_wrt_iff,
assert_of_bnot,
iff_weakening_uiff,
iff_transitivity,
dcdr-to-bool-equivalence,
and_functionality_wrt_iff,
or_functionality_wrt_iff,
member_append,
eqff_to_assert,
eqtt_to_assert,
bool_wf,
filter_is_sublist
\mforall{}[A:Type]
\mforall{}eq:EqDecider(A)
\mforall{}[B:A {}\mrightarrow{} Type]
\mforall{}f:a:A fp-> B[a]
\mforall{}[P:A {}\mrightarrow{} \mBbbP{}]
((\mforall{}a:A. Dec(P[a]))
{}\mRightarrow{} (\mexists{}fp,fnp:a:A fp-> B[a]
((f \msubseteq{} fp \moplus{} fnp \mwedge{} fp \moplus{} fnp \msubseteq{} f)
\mwedge{} ((\mforall{}a:A. P[a] supposing \muparrow{}a \mmember{} dom(fp)) \mwedge{} (\mforall{}a:A. \mneg{}P[a] supposing \muparrow{}a \mmember{} dom(fnp)))
\mwedge{} fpf-domain(fp) \msubseteq{} fpf-domain(f)
\mwedge{} fpf-domain(fnp) \msubseteq{} fpf-domain(f))))
Date html generated:
2012_01_23-AM-11_54_49
Last ObjectModification:
2011_12_10-AM-11_54_42
Home
Index