Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). b ). b a a   ( (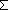 i:{a..b i:{a..b }. e(i)) = 0 }. e(i)) = 0 | [sum_via_intseg_null] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). b ). b a a   ( (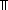 i:{a..b i:{a..b }. e(i)) = 1 }. e(i)) = 1 | [mul_via_intseg_null] |
Thm*  m,k: m,k: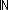 . m . m k k   k!m = ((k!) k!m = ((k!) 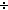 ((k-m)!)) ((k-m)!)) | [factorial_ratio2] |
Thm*  m,k: m,k: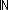 . m . m k k   k! = (k-m)! k! = (k-m)!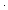 k!m k!m | [factorial_ratio] |
Thm*  k: k: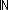 . k! . k! 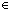 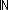 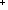 | [factorial_via_iter_wf] |
Thm*  m,k: m,k: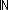 . 1 . 1  m m  k k   k!m = k k!m = k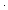 (k-1)!(m-1) (k-1)!(m-1) 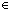 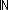 | [factorial_tail_via_iter_step_rw] |
Thm*  m,k: m,k: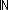 . 1 . 1  m m  k k   ( ( k',m': k',m':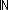 . k' = k-1 . k' = k-1   m' = m-1 m' = m-1   k!m = k k!m = k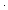 k'!m' k'!m' 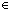 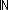 ) ) | [factorial_tail_via_iter_step] |
Thm*  m,k: m,k: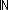 . k<m . k<m   k!m = 0 k!m = 0 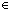 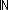 | [factorial_tail_via_iter_zero] |
Thm*  m,k: m,k: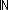 . m = 0 . m = 0 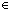 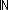   k!m = 1 k!m = 1 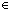 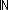 | [factorial_tail_via_iter_null] |
Thm*  n,m,k: n,m,k: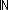 . n . n k-m k-m   m m k k   k!(n+m) = (k-m)!n k!(n+m) = (k-m)!n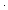 k!m k!m | [factorial_tail_split_mid] |
Thm*  m,k: m,k: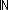 . k!m . k!m 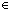 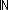 | [factorial_tail_via_iter_wf] |
Thm* (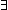 i:{a..b i:{a..b }. e(i) = 0) }. e(i) = 0)   ( (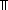 i:{a..b i:{a..b }. e(i)) = 0 }. e(i)) = 0 | [zero_ann_iter_via_intseg] |
Thm* (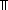 i:{a..b i:{a..b }. e(i)) = 0 }. e(i)) = 0 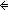  ( (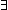 i:{a..b i:{a..b }. e(i) = 0) }. e(i) = 0) | [iter_prod_zero_iff_factor_zero] |
Thm*  e:({a..b e:({a..b } }  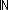 ). ( ). (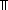 i:{a..b i:{a..b }. e(i)) = 1 }. e(i)) = 1 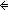  ( ( i:{a..b i:{a..b }. e(i) = 1) }. e(i) = 1) | [iter_nat_prod_one_iff_factors_one] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). ( Prop). (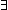 i:{a..b i:{a..b }. P(i)) }. P(i)) 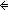  (Or i:{a..b (Or i:{a..b }. P(i)) }. P(i)) | [exist_intseg_vs_iter_or] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). b Prop). b a a   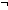 ( (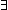 i:{a..b i:{a..b }. P(i)) }. P(i)) | [exist_intseg_null] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). Prop).
Thm* a<b   (( ((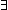 i:{a..b i:{a..b }. P(i)) }. P(i)) 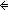  ( (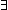 i:{a..(b-1) i:{a..(b-1) }. P(i)) }. P(i)) 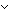 P(b-1)) P(b-1)) | [or_via_exist_intseg_split_last] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). Prop).
Thm* a<b
Thm*  
Thm* ( c: c: . b = c+1 . b = c+1   (( ((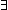 i:{a..b i:{a..b }. P(i)) }. P(i)) 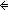  ( (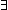 i:{a..c i:{a..c }. P(i)) }. P(i)) 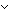 P(c))) P(c))) | [or_via_exist_intseg_notnull] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). ( Prop). ( i:{a..b i:{a..b }. P(i)) }. P(i)) 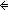  (And i:{a..b (And i:{a..b }. P(i)) }. P(i)) | [all_intseg_vs_iter_and] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). Prop).
Thm* a<b   (( (( i:{a..b i:{a..b }. P(i)) }. P(i)) 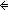  ( ( i:{a..(b-1) i:{a..(b-1) }. P(i)) & P(b-1)) }. P(i)) & P(b-1)) | [and_via_all_intseg_split_last] |
Thm*  a,b: a,b: , P:({a..b , P:({a..b } }  Prop). Prop).
Thm* a<b
Thm*  
Thm* ( c: c: . b = c+1 . b = c+1   (( (( i:{a..b i:{a..b }. P(i)) }. P(i)) 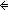  ( ( i:{a..c i:{a..c }. P(i)) & P(c))) }. P(i)) & P(c))) | [and_via_all_intseg_notnull] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a<b   ( (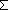 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (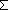 i:{a..b-1 i:{a..b-1 }. e(i))+e(b-1) }. e(i))+e(b-1) | [sum_via_intseg_split_last] |
Thm*  a,b,c: a,b,c: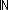 . (a . (a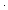 b) b)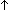 c = a c = a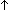 c c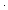 b b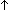 c c | [exp_reduce1] |
Thm*  a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ). ).
Thm* (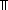 i:{a..b i:{a..b }. f(i)) }. f(i)) ( (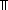 i:{a..b i:{a..b }. g(i)) = ( }. g(i)) = (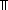 i:{a..b i:{a..b }. f(i) }. f(i) g(i)) g(i)) | [mul_via_intseg_factors] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a<b   ( (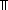 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (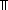 i:{a..b-1 i:{a..b-1 }. e(i)) }. e(i))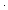 e(b-1) e(b-1) | [mul_via_intseg_split_last] |
Thm*  i: i: , x,y: , x,y: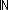 . i . i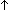 x x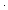 i i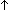 y = i y = i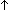 (x+y) (x+y) | [sum_exponent] |
Thm*  a,c,b: a,c,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a c c
Thm*  
Thm* c b b   ( (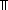 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (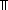 i:{a..c i:{a..c }. e(i)) }. e(i))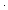 ( (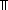 i:{c..b i:{c..b }. e(i)) }. e(i)) | [mul_via_intseg_split_mid] |
Thm*  a,c,b: a,c,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a c c
Thm*  
Thm* c b b   ( (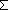 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (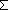 i:{a..c i:{a..c }. e(i))+( }. e(i))+(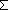 i:{c..b i:{c..b }. e(i)) }. e(i)) | [sum_via_intseg_split_mid] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ), i:{a..b ), i:{a..b }. e(i) | ( }. e(i) | (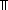 i:{a..b i:{a..b }. e(i)) }. e(i)) | [components_divide_iter_mul] |
Thm*  a,c,b: a,c,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a c c
Thm*  
Thm* c<b
Thm*  
Thm* (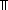 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (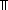 i:{a..c i:{a..c }. e(i)) }. e(i))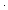 e(c) e(c)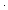 ( (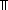 i:{c+1..b i:{c+1..b }. e(i)) }. e(i)) | [mul_via_intseg_split_pluck] |
Thm*  a,c,b: a,c,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a c c
Thm*  
Thm* c<b
Thm*  
Thm* (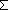 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (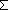 i:{a..c i:{a..c }. e(i))+e(c)+( }. e(i))+e(c)+(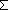 i:{c+1..b i:{c+1..b }. e(i)) }. e(i)) | [sum_via_intseg_split_pluck] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,c,b: a,c,b: , e:({a..b , e:({a..b } }  A). A).
Thm* (a c c
Thm* ( 
Thm* (c<b
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) }. e(i))
Thm* (=
Thm* (f((Iter(f;u) i:{a..c }. e(i)),f(e(c),Iter(f;u) i:{c+1..b }. e(i)),f(e(c),Iter(f;u) i:{c+1..b }. e(i)))) }. e(i)))) | [iter_via_intseg_split_pluck] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,b: a,b: , c:{a...b}, d:{c..b , c:{a...b}, d:{c..b }, e:({a..b }, e:({a..b } }  A). A).
Thm* (( i:{a..b i:{a..b }. i<c }. i<c 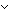 d d i i   e(i) = u) e(i) = u)
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) = (Iter(f;u) i:{c..d }. e(i)) = (Iter(f;u) i:{c..d }. e(i))) }. e(i))) | [iter_via_intseg_amputate_units] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,c,b: a,c,b: , e:({a..b , e:({a..b } }  A). A).
Thm* (a c c
Thm* ( 
Thm* (c b b
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) }. e(i))
Thm* (=
Thm* (f((Iter(f;u) i:{a..c }. e(i)),Iter(f;u) i:{c..b }. e(i)),Iter(f;u) i:{c..b }. e(i))) }. e(i))) | [iter_via_intseg_split_mid] |
Thm*  a,b: a,b: , f,g:({a..b , f,g:({a..b } }   ). ).
Thm* (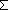 i:{a..b i:{a..b }. f(i))+( }. f(i))+(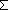 i:{a..b i:{a..b }. g(i)) = ( }. g(i)) = (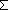 i:{a..b i:{a..b }. f(i)+g(i)) }. f(i)+g(i)) | [add_via_intseg_addends] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_commutative_sep(A; f)
Thm*  
Thm* is_ident(A; f; u)
Thm*  
Thm* is_assoc_sep(A; f)
Thm*  
Thm* ( a,b: a,b: , e,g:({a..b , e,g:({a..b } }  A). A).
Thm* (f((Iter(f;u) i:{a..b }. e(i)),Iter(f;u) i:{a..b }. e(i)),Iter(f;u) i:{a..b }. g(i)) }. g(i))
Thm* (=
Thm* ((Iter(f;u) i:{a..b }. f(e(i),g(i))) }. f(e(i),g(i)))
Thm* (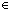 A) A) | [iter_via_intseg_comp_binop] |
Thm*  f:(A f:(A  A A  A), u:A, a,b,c,d: A), u:A, a,b,c,d: . .
Thm* b-a = d-c
Thm*  
Thm* ( e:({a..b e:({a..b } }  A), g:({c..d A), g:({c..d } }  A). A).
Thm* (( i:{a..b i:{a..b }, j:{c..d }, j:{c..d }. j-i = c-a }. j-i = c-a   e(i) = g(j) e(i) = g(j) 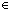 A) A)
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) = (Iter(f;u) j:{c..d }. e(i)) = (Iter(f;u) j:{c..d }. g(j))) }. g(j))) | [iter_via_intseg_shift] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A), k: A), k: . .
Thm* (Iter(f;u) i:{a..b }. e(i)) = (Iter(f;u) j:{a+k..b+k }. e(i)) = (Iter(f;u) j:{a+k..b+k }. e(j-k)) }. e(j-k)) | [iter_via_intseg_shift_rw] |
Thm*  x: x: . 1 . 1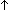 x = 1 x = 1 | [one_exponentiation] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). ( ). ( i:{a..b i:{a..b }. e(i) = 1) }. e(i) = 1)   ( (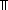 i:{a..b i:{a..b }. e(i)) = 1 }. e(i)) = 1 | [mul_via_intseg_one] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* ( a,b: a,b: , e:({a..b , e:({a..b } }  A). A).
Thm* (( i:{a..b i:{a..b }. e(i) = u) }. e(i) = u)   (Iter(f;u) i:{a..b (Iter(f;u) i:{a..b }. e(i)) = u) }. e(i)) = u) | [iter_via_intseg_all_units] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A). A).
Thm* a<b
Thm*  
Thm* (Iter(f;u) i:{a..b }. e(i)) = f((Iter(f;u) i:{a..b-1 }. e(i)) = f((Iter(f;u) i:{a..b-1 }. e(i)),e(b-1)) }. e(i)),e(b-1)) | [iter_via_intseg_split_last] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a<b   ( ( c: c: . b = c+1 . b = c+1   ( (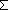 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (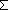 i:{a..c i:{a..c }. e(i))+e(c)) }. e(i))+e(c)) | [sum_via_intseg_notnull] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). ).
Thm* a<b   ( ( c: c: . b = c+1 . b = c+1   ( (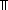 i:{a..b i:{a..b }. e(i)) = ( }. e(i)) = (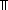 i:{a..c i:{a..c }. e(i)) }. e(i))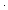 e(c)) e(c)) | [mul_via_intseg_notnull] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A). A).
Thm* a<b
Thm*  
Thm* ( c: c: . .
Thm* (b = c+1
Thm* ( 
Thm* ((Iter(f;u) i:{a..b }. e(i)) = f((Iter(f;u) i:{a..c }. e(i)) = f((Iter(f;u) i:{a..c }. e(i)),e(c))) }. e(i)),e(c))) | [iter_via_intseg_notnull] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). a+1 = b ). a+1 = b   ( (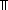 i:{a..b i:{a..b }. e(i)) = e(a) }. e(i)) = e(a) | [mul_via_intseg_singleton] |
Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ). a+1 = b ). a+1 = b   ( (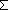 i:{a..b i:{a..b }. e(i)) = e(a) }. e(i)) = e(a) | [sum_via_intseg_singleton] |
Thm*  f:(A f:(A  A A  A), u:A. A), u:A.
Thm* is_ident(A; f; u)
Thm*  
Thm* ( a,b: a,b: , e:({a..b , e:({a..b } }  A). a+1 = b A). a+1 = b   (Iter(f;u) i:{a..b (Iter(f;u) i:{a..b }. e(i)) = e(a)) }. e(i)) = e(a)) | [iter_via_intseg_singleton] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A). A).
Thm* b a a   (Iter(f;u) i:{a..b (Iter(f;u) i:{a..b }. e(i)) = (Iter(f;u) i:{a..a }. e(i)) = (Iter(f;u) i:{a..a }. e(i)) }. e(i)) | [iter_via_intseg_nullnorm] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A). A).
Thm* b a a   (Iter(f;u) i:{a..b (Iter(f;u) i:{a..b }. e(i)) = u }. e(i)) = u | [iter_via_intseg_null] |
Thm*  x: x: . x . x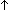 1 = x 1 = x | [exponent_one] |
Thm*  x: x: . x . x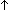 0 = 1 0 = 1 | [exponent_zero] |
Thm*  f:(A f:(A  A A  A), u:A, a,b: A), u:A, a,b: , e:({a..b , e:({a..b } }  A). (Iter(f;u) i:{a..b A). (Iter(f;u) i:{a..b }. e(i)) }. e(i)) 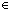 A A | [iter_via_intseg_wf] |
Thm*  P:( P:(      Prop). Prop).
Thm* ( a: a: , b:{...a}. P(a,b)) , b:{...a}. P(a,b))
Thm*  
Thm* ( a: a: , b:{a+1...}. ( , b:{a+1...}. ( c:{a..b c:{a..b }. P(a,c)) }. P(a,c))   P(a,b)) P(a,b))   ( ( a,b: a,b: . P(a,b)) . P(a,b)) | [all_int_segs_by_upper_ind] |
Thm*  P:( P:(      Prop), a: Prop), a: . .
Thm* ( b:{...a}. P(a,b)) b:{...a}. P(a,b))
Thm*  
Thm* ( b:{a+1...}. ( b:{a+1...}. ( c:{a..b c:{a..b }. P(a,c)) }. P(a,c))   P(a,b)) P(a,b))   ( ( b: b: . P(a,b)) . P(a,b)) | [int_segs_from_base_by_upper_ind] |
Thm*  P:( P:(      Prop), a: Prop), a: . .
Thm* ( b:{...a}. P(a,a) b:{...a}. P(a,a)   P(a,b)) P(a,b))   ( ( b:{a...}. P(a,b)) b:{a...}. P(a,b))   ( ( b: b: . P(a,b)) . P(a,b)) | [split_int_domain_by_norm_lower] |
Thm*  P:( P:(      Prop), a: Prop), a: . .
Thm* ( b:{a...}. ( b:{a...}. ( c:{a..b c:{a..b }. P(a,c)) }. P(a,c))   P(a,b)) P(a,b))   ( ( b:{a...}. P(a,b)) b:{a...}. P(a,b)) | [int_seg_upper_ind] |
Thm*  P:( P:(      Prop). Prop).
Thm* ( a: a: , b:{...a}. P(a,b)) , b:{...a}. P(a,b))
Thm*  
Thm* ( a: a: . ( . ( b:{...a}. P(a,b)) b:{...a}. P(a,b))   ( ( b:{a...}. P(a,b))) b:{a...}. P(a,b)))   ( ( a,b: a,b: . P(a,b)) . P(a,b)) | [all_int_pairs_via_all_splits] |
Thm*  P:( P:(      Prop), a: Prop), a: . .
Thm* ( b:{...a}. P(a,b)) b:{...a}. P(a,b))
Thm*  
Thm* (( b:{...a}. P(a,b)) b:{...a}. P(a,b))   ( ( b:{a...}. P(a,b))) b:{a...}. P(a,b)))   ( ( b: b: . P(a,b)) . P(a,b)) | [split_int_domain] |
Thm*  f:(A f:(A  A A  A). is_commutative_sep(A; f) A). is_commutative_sep(A; f) 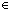 Prop Prop | [is_commutative_sep_wf] |
Thm*  f:(A f:(A  A A  A). is_commutative(A; x,z.f(x,z)) A). is_commutative(A; x,z.f(x,z)) 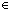 Prop Prop | [is_commutative_wf] |
Thm*  f:(A f:(A  A A  A). is_assoc_sep(A; f) A). is_assoc_sep(A; f) 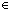 Prop Prop | [is_assoc_sep_wf] |
Thm*  f:(A f:(A  A A  A), u,v:A. is_ident(A; f; u) A), u,v:A. is_ident(A; f; u)   is_ident(A; f; v) is_ident(A; f; v)   u = v u = v | [binary_ident_unique] |
Thm*  f:(A f:(A  A A  A), u:A. is_ident(A; f; u) A), u:A. is_ident(A; f; u) 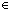 Prop Prop | [is_ident_wf] |
Def is_commutative(A; x,z.f(x;z)) ==  x,z:A. f(x;z) = f(z;x) x,z:A. f(x;z) = f(z;x) 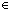 A A | [is_commutative] |
Def is_assoc(A; x,z.f(x;z)) ==  x,y,z:A. f(x;f(y;z)) = f(f(x;y);z) x,y,z:A. f(x;f(y;z)) = f(f(x;y);z) 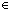 A A | [is_assoc] |
Def is_ident(A; f; u) ==  x:A. f(u,x) = x & f(x,u) = x x:A. f(u,x) = x & f(x,u) = x | [is_ident] |