Thm*  p:( p:( a {k} a {k}  ). {i: ). {i: a| p(i) } ~ a| p(i) } ~  k k | [card_st_sized_bool] |
Thm*  p:( p:( a a   ). {x: ). {x: a| p(x) } ~ a| p(x) } ~  ( ( size( size( a)(p)) a)(p)) | [card_st_vs_boolsize] |
Thm*  f:( f:( a a   2). 2).
Thm* ( i: i: a. P(i) a. P(i)   f(i) = 1 f(i) = 1   2) 2)   ({x: ({x: a| P(x) } ~ a| P(x) } ~  (Msize(f))) (Msize(f))) | [card_st_vs_msize] |
Thm* ( a {k} a {k}  ) ~ ( ) ~ ( a {k} a {k}  2) 2) | [card_boolset_vs_mset] |
Thm*  a,k: a,k: . .  a {k} a {k}   Type Type | [sized_bool_wf] |
Thm*  a: a: . .  size( size( a) a)  ( ( a a   ) )   | [boolsize_wf] |
Thm*  a,k,x: a,k,x: . .  a {k} a {k} {x...} {x...}  Type Type | [sized_mset_wf5] |
Thm*  a,k: a,k: . .  a {k} a {k}    Type Type | [sized_mset_wf4] |
Thm*  a,k,x: a,k,x: , y: , y: . .  a {k} a {k} {x...y} {x...y}  Type Type | [sized_mset_wf3] |
Thm*  a,k,x: a,k,x: , y: , y: . .  a {k} a {k} {x..y {x..y } }  Type Type | [sized_mset_wf2] |
Thm*  a,k: a,k: . .  a {k} a {k}   Type Type | [sized_mset_wf] |
Thm*  k: k: . Msize . Msize  ( ( k k   ) )   | [msize_wf] |
Thm* ( a bij a bij  a) ~ ( a) ~ ( a a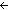   a) a) | [nsub_bij_ooc_invpair] |
Thm* ( k inj k inj  k) ~ ( k) ~ ( k onto k onto  k) k) | [nsub_inj_ooc_nsub_surj] |
Thm* ( k inj k inj  k) ~ ( k) ~ ( k bij k bij  k) k) | [nsub_inj_ooc_nsub_bij] |
Thm* ( k inj k inj  k) =ext ( k) =ext ( k bij k bij  k) k) | [nsub_inj_exteq_nsub_bij] |
Thm* ( k onto k onto  k) ~ ( k) ~ ( k bij k bij  k) k) | [nsub_surj_ooc_nsub_bij] |
Thm* ( k onto k onto  k) =ext ( k) =ext ( k bij k bij  k) k) | [nsub_surj_exteq_nsub_bij] |
Thm* ( k inj k inj  k) =ext ( k) =ext ( k onto k onto  k) k) | [nsub_inj_exteq_nsub_surj] |
Thm* (  ( ( a onto a onto  b)) b))   b b a a | [surj_typing_imp_le] |
Thm* (  ( ( a onto a onto  b)) b))   ( (  ( ( b inj b inj  a)) a)) | [nsub_surj_imp_a_rev_inj2] |
Thm*  f:( f:( a bij a bij  a). InvFuns( a). InvFuns( a; a; a;f; a;f; y.least x: y.least x: . f(x)= . f(x)= y) y) | [nsub_bij_least_preimage_inverse] |
Thm*  f:( f:( a onto a onto  b). ( b). ( y.least x: y.least x: . f(x)= . f(x)= y) y)   b inj b inj  a a | [nsub_surj_imp_a_rev_inj] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)
Thm*  
Thm* ( a: a: , f:( , f:( a onto a onto B). ( B). ( y.least x: y.least x: . (f(x)) e y) . (f(x)) e y)  B inj B inj  a) a) | [nsub_surj_imp_a_rev_inj_gen] |
Thm* InvFuns(A;A;f;g)   ( ( i: i: . InvFuns(A;A;f{ . InvFuns(A;A;f{ i};g{ i};g{ i})) i})) | [compose_iter_inverses] |
Thm* Bij(A; A; f)   ( ( i: i: . Bij(A; A; f{ . Bij(A; A; f{ i})) i})) | [compose_iter_bijection] |
Thm* Surj(A; A; f)   ( ( i: i: . Surj(A; A; f{ . Surj(A; A; f{ i})) i})) | [compose_iter_surjection] |
Thm*  f:(A inj f:(A inj A), i: A), i: . f{ . f{ i} i}  A inj A inj A A | [compose_iter_injection2] |
Thm*  k: k: , f:( , f:( k inj k inj  k). k).  i: i:  . f{ . f{ i} = Id i} = Id   k k   k k | [iter_perm_cycles_uniform2] |
Thm*  k: k: , f:( , f:( k inj k inj  k). k).  i: i:  . .  u: u: k. f{ k. f{ i}(u) = u i}(u) = u | [iter_perm_cycles_uniform] |
Thm*  k: k: , f:( , f:( k inj k inj  k), u: k), u: k. k.  i: i:  . f{ . f{ i}(u) = u i}(u) = u | [compose_iter_inj_cycles] |
Thm* Inj(A; A; f)   ( ( i: i: . Inj(A; A; f{ . Inj(A; A; f{ i})) i})) | [compose_iter_injection] |
Thm*  x:A, f:(A x:A, f:(A  A), i,j: A), i,j: . f{ . f{ i}{ i}{ j}(x) = f{ j}(x) = f{ i i j}(x) j}(x) | [compose_iter_prod2] |
Thm*  x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i . k = i j j   f{ f{ i}{ i}{ j}(x) = f{ j}(x) = f{ k}(x) k}(x)  A A | [compose_iter_prod] |
Thm*  f:(A f:(A  A), k: A), k: , i:{0...k}. f{ , i:{0...k}. f{ k} = f{ k} = f{ i} o f{ i} o f{ k-i} k-i} | [compose_iter_sum_comp_rw] |
Thm*  x:A, f:(A x:A, f:(A  A), k: A), k: , i:{0...k}. f{ , i:{0...k}. f{ k}(x) = f{ k}(x) = f{ i}(f{ i}(f{ k-i}(x)) k-i}(x)) | [compose_iter_sum_rw] |
Thm*  f:(A f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i} o f{ i} o f{ j} = f{ j} = f{ k} k} | [compose_iter_sum_comp] |
Thm*  x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i}(f{ i}(f{ j}(x)) = f{ j}(x)) = f{ k}(x) k}(x) | [compose_iter_sum] |
Thm*  i: i: . Id{ . Id{ i} = Id i} = Id  A A  A A | [compose_iter_id] |
Thm*  f:(A f:(A  A), u:A. f(u) = u A), u:A. f(u) = u   ( ( i: i: . f{ . f{ i}(u) = u) i}(u) = u) | [compose_iter_point_id] |
Thm* (k:   k k   ) ~ ) ~  | [card_nat_vs_nat_tuples_all] |
Thm* (k:    k k   ) ~ ) ~  | [card_nat_vs_nat_tuples] |
Thm*  k: k:  . ( . ( k k   ) ~ ) ~  | [card_nat_vs_nat_tuple] |
Thm* (   ) ~ ) ~  | [card_nat_vs_nat_nat] |
Thm*  f:(A f:(A  A), i: A), i: . f{ . f{ i} i}  A A  A A | [compose_iter_wf] |
Thm* Bij( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) | [nat_to_nat_pair_bij] |
Thm* Surj( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) | [nat_to_nat_pair_surj] |
Thm* Inj( ; ;    ; nat_to_nat_pair) ; nat_to_nat_pair) | [nat_to_nat_pair_inj] |
Thm* nat_to_nat_pair        | [nat_to_nat_pair_wf] |
Thm* InvFuns(   ;{xy:( ;{xy:(   )| )|  xy = <0,0> xy = <0,0>     };next_nat_pair;prev_nat_pair) };next_nat_pair;prev_nat_pair) | [next_nat_pair_vs_prev_nat_pair] |
Thm* prev_nat_pair  {xy:( {xy:(   )| )|  xy = <0,0> xy = <0,0>     } }     | [prev_nat_pair_wf] |
Thm* Inj(   ; ;    ; next_nat_pair) ; next_nat_pair) | [next_nat_pair_inj] |
Thm*  xy:( xy:(   ). ).  <0,0> = next_nat_pair(xy) <0,0> = next_nat_pair(xy)     | [next_nat_pair_not_zeroes] |
Thm* next_nat_pair          | [next_nat_pair_wf] |
Thm*  a: a: , b:( , b:( a a   ). (i: ). (i: a a  b(i)) ~ b(i)) ~  ( (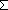 i: i: a. b(i)) a. b(i)) | [card_sigma_vs_nsub_sigma] |
Thm*  a,b: a,b: . ( . ( a+ a+ b) ~ b) ~  (a+b) (a+b) | [nsub_add_rw] |
Thm*  a,b,c: a,b,c: . c . c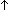 (a (a b) = (c b) = (c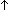 a) a)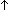 b b | [exp_exp_reduce2] |
Thm*  a,b,c: a,b,c: . c . c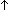 (a (a b) = (c b) = (c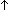 b) b)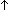 a a | [exp_exp_reduce1] |
Thm*  a,b: a,b: . ( . ( a a   b) ~ b) ~  (b (b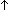 a) a) | [card_fun_vs_nsub_exp] |
Thm*  a: a: , b:( , b:( a a   ). (i: ). (i: a a   b(i)) ~ b(i)) ~  ( (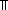 i: i: a. b(i)) a. b(i)) | [card_pi_vs_nsub_pi] |
Thm* ( k inj k inj  k) ~ k) ~  (k!) (k!) | [nsub_inj_factorial] |
Thm* ( a inj a inj  b) ~ b) ~  (b!a) (b!a) | [nsub_inj_factorial_tail] |
Thm* ( b inj b inj  b) ~ b) ~  (b!) (b!) | [nsub_inj_factorial2] |
Thm*  a,b: a,b: . (A ~ . (A ~  a) a)   (B ~ (B ~  b) b)   ((A ((A B) ~ B) ~  (a (a b)) b)) | [finite_indep_sum_card] |
Thm*  a,b,c: a,b,c: . a . a (b (b c) = (a c) = (a b) b) c c | [mul_assoc_from_cross_assoc] |
Thm*  a,b: a,b: . ( . ( a a  b) ~ b) ~  (a (a b) b) | [nsub_mul_rw] |
Thm*  a,b,c: a,b,c: . a . a b = c b = c   (( (( a a  b) ~ b) ~  c) c) | [nsub_mul] |
Thm*  c,a,b: c,a,b: . a+b = c . a+b = c     (( (( a+ a+ b) ~ b) ~  c) c) | [nsub_add] |
Thm*  Finite( Finite( ) ) | [nat_not_finite] |
Thm*  a,b: a,b: . ( . ( a ~ a ~  b) b)   a = b a = b | [fin_card_vs_nat_eq] |
Thm* (A ~  m) m)   (A ~ (A ~  k) k)   m = k m = k | [counting_is_unique] |
Thm*  (( ((    ) ~ ) ~  ) ) | [not_nat_occ_natfuns] |
Thm*  k: k: . .  Infinite( Infinite( k) k) | [nsub_not_infinite] |
Thm*  ~ ~  | [int_ooc_nat] |
Thm*  k: k: , B:( , B:( k k  Type), Q:(x: Type), Q:(x: k k  B(x) B(x)  Prop). Prop).
Thm* ( x: x: k. k.  y:B(x). Q(x;y)) y:B(x). Q(x;y))   ( ( f:(x: f:(x: k k  B(x)). B(x)).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) | [dep_finite_choice] |
Thm*  k: k: , Q:( , Q:( k k  A A  Prop). Prop).
Thm* ( x: x: k. k.  y:A. Q(x;y)) y:A. Q(x;y))   ( ( f:( f:( k k  A). A).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) | [finite_choice] |
Thm*  f:( f:( a onto a onto  b). Surj( b). Surj( a; a;  b; f) b; f) | [surjection_type_nsub_surjection] |
Thm*  f:(A onto f:(A onto B), a: B), a: . .  a onto a onto A A   (B Discrete) (B Discrete)   Surj(A; B; f) Surj(A; B; f) | [surjection_type_surjection] |
Thm*  a,b: a,b: . (a -- b) . (a -- b)   | [ndiff_wf_nat] |
Thm*  k: k:  . k! = k . k! = k (k-1)! (k-1)!   | [factorial_via_intseg_step_rw] |
Thm*  k,n: k,n: . k = n+1 . k = n+1   k! = k k! = k n! n!   | [factorial_via_intseg_step] |
Thm*  P:{P:( P:{P:(   Prop)| Prop)|  i: i: . P(i) }. . P(i) }.
Thm* ( i: i: . Dec(P(i))) . Dec(P(i)))   ( (  {i: {i: | P(i) & ( | P(i) & ( j: j: . j<i . j<i    P(j)) }) P(j)) }) | [least_exists2] |
Thm*  k: k: , P:{P:( , P:{P:( k k  Prop)| Prop)|  i: i: k. P(i) }. k. P(i) }.
Thm* ( i: i: k. Dec(P(i))) k. Dec(P(i)))   ( (  {i: {i: k| P(i) & ( k| P(i) & ( j: j: i. i.  P(j)) }) P(j)) }) | [least_exists] |
Thm*  k: k: , j: , j: k. {i: k. {i: k| k|  i = j } ~ i = j } ~  (k-1) (k-1) | [nsub_delete_rw] |
Thm*  k: k: , j: , j: k, m: k, m: . m = k-1 . m = k-1   ({i: ({i: k| k|  i = j } ~ i = j } ~  m) m) | [nsub_delete] |
Thm*  k: k: . Finite( . Finite( k) k) | [nsub_is_finite] |
Thm*   ~ ~  | [nat_plus_ooc_nat] |
Thm*  k: k: . ( . ( k+ k+ ) ~ ) ~  | [fin_plus_nat_ooc_nat] |
Thm*  f:( f:( a onto a onto  b), y: b), y: b. f(least x: b. f(least x: . f(x)= . f(x)= y) = y y) = y | [nsub_surj_least_preimage_works] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. f(least x: B), y:B. f(least x: . (f(x)) e y) = y) . (f(x)) e y) = y) | [nsub_surj_least_preimage_works_gen] |
Thm*  f:( f:( a onto a onto  b), y: b), y: b. (least x: b. (least x: . f(x)= . f(x)= y) y)   a a | [nsub_surj_least_preimage_total] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. (least x: B), y:B. (least x: . (f(x)) e y) . (f(x)) e y)   a) a) | [nsub_surj_least_preimage_total_gen] |
Thm* (A Discrete)   ( ( k: k: , f:( , f:( k inj k inj A). f A). f   k bij k bij {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) | [nsub_inj_discr_range_bijtype] |
Thm* (A Discrete)
Thm*  
Thm* ( k: k: , f:( , f:( k inj k inj A). A).
Thm* ({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
Thm* (& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
Thm* (& Bij( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) | [nsub_inj_discr_range_bij] |
Thm* (A Discrete)   ( ( k: k: , f:( , f:( k k  A). f A). f   k onto k onto {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) | [nsub_discr_range_surjtype] |
Thm* (A Discrete)
Thm*  
Thm* ( k: k: , f:( , f:( k k  A). A).
Thm* ({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
Thm* (& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
Thm* (& Surj( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) | [nsub_discr_range_surj] |
Thm*  p:{p:( p:{p:(    )| )|  i: i: . p(i) }. p(least i: . p(i) }. p(least i: . p(i)) . p(i)) | [least_satisfies2] |
Thm*  p:{p:( p:{p:(    )| )|  i: i: . p(i) }, j: . p(i) }, j: (least i: (least i: . p(i)). . p(i)).  p(j) p(j) | [least_is_least2] |
Thm*  k: k: , p:{p:( , p:{p:( k k   )| )|  i: i: k. p(i) }, j: k. p(i) }, j: (least i: (least i: . p(i)). . p(i)).  p(j) p(j) | [least_is_least] |
Thm*  k: k: , p:{p:( , p:{p:( k k   )| )|  i: i: k. p(i) }. p(least i: k. p(i) }. p(least i: . p(i)) . p(i)) | [least_satisfies] |
Thm*  p:{p:( p:{p:(    )| )|  i: i: . p(i) }. (least i: . p(i) }. (least i: . p(i)) . p(i))   | [least_wf2] |
Thm*  p:{p:( p:{p:(    )| )|  i: i: . p(i) }. . p(i) }.
Thm* (least i: . p(i)) . p(i))  {i: {i: | p(i) & ( | p(i) & ( j: j: . j<i . j<i    p(j)) } p(j)) } | [least_characterized2] |
Thm*  k: k: , p:{p:( , p:{p:( k k   )| )|  i: i: k. p(i) }. (least i: k. p(i) }. (least i: . p(i)) . p(i))   k k | [least_wf] |
Thm*  k: k: , p:{p:( , p:{p:( k k   )| )|  i: i: k. p(i) }. k. p(i) }.
Thm* (least i: . p(i)) . p(i))  {i: {i: k| p(i) & ( k| p(i) & ( j: j: i. i.  p(j)) } p(j)) } | [least_characterized] |
Thm*  m,k: m,k: , f:( , f:( m m   k). k<m k). k<m   ( ( x,y: x,y: m. x m. x 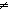 y & f(x) = f(y)) y & f(x) = f(y)) | [pigeon_hole] |
Thm*  m,k: m,k: , f:( , f:( m m   k). Inj( k). Inj( m; m;  k; f) k; f)   m m k k | [inj_imp_le2] |
Thm* (  ( ( m inj m inj  k)) k))   m m k k | [inj_typing_imp_le] |
Thm* ( f:( f:( m m   k). Inj( k). Inj( m; m;  k; f)) k; f))   m m k k | [inj_imp_le] |
Thm*  m: m: , f:( , f:( m m   ). ).  Inj( Inj( m; m;  ; f) ; f)   ( ( x: x: m, y: m, y: x. f(x) = f(y)) x. f(x) = f(y)) | [finite_inj_counter_example] |
Thm* Bij( (m+1); (m+1);  (k+1); f) (k+1); f)   Bij( Bij( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) | [delete_fenum_value_is_fenum] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)   Inj( Inj( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) | [delete_fenum_value_is_inj] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
Thm*  
Thm* ( i: i: m. m.  f(i) = k f(i) = k   (Replace value k by f(m) in f)(i) = f(i) (Replace value k by f(m) in f)(i) = f(i)   k) k) | [delete_fenum_value_comp2] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
Thm*  
Thm* ( i: i: m. f(i) = k m. f(i) = k   (Replace value k by f(m) in f)(i) = f(m) (Replace value k by f(m) in f)(i) = f(m)   k) k) | [delete_fenum_value_comp1] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)   (Replace value k by f(m) in f) (Replace value k by f(m) in f)   m m   k k | [delete_fenum_value_wf] |
Thm*  a: a:  , b: , b: , j: , j: b, f:( b, f:( (a-1) inj (a-1) inj {x: {x: b| b|  x = j }). x = j }).
Thm* ( i.if i= i.if i= a-1 a-1 j else f(i) fi) j else f(i) fi)   a inj a inj  b b | [nsub_inj_fill_typing] |
Thm*  a: a:  , b: , b: , f:( , f:( a inj a inj  b). f b). f   (a-1) inj (a-1) inj {x: {x: b| b|  x = f(a-1) } x = f(a-1) } | [nsub_inj_lop_typing] |
Thm*  i,j: i,j: . Dec(i = j) . Dec(i = j) | [decidable__nat_equal] |
Thm* IsEqFun( b; b;  i,j. i= i,j. i= j) j) | [eq_int_is_eq_nsub] |
Def  a {k} a {k}  == {p:( == {p:( a a   )| )|  size( size( a)(p) = k } a)(p) = k } | [sized_bool] |
Def  a {k} a {k} T == {p:( T == {p:( a a  T)| Msize(p) = k } T)| Msize(p) = k } | [sized_mset] |
Def Infinite(A) ==   ( ( inj inj A) A) | [productively_infinite] |
Def Unbounded(A) ==  k: k: . .   ( ( k inj k inj A) A) | [unboundedly_infinite] |
Def fin_enum(A) == k:   k k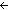  A A | [fin_enum] |
Def Finite(A) ==  n: n: . A ~ . A ~  n n | [is_finite_type] |