Thm* (AH ~  8) 8)   ((AH ((AH {1...8}) ~ {1...8}) ~  64) 64) | [chessboard_example] |
Thm*  x:A. (x x:A. (x  nil) nil)   False False | [is_list_mem_null] |
Thm*  f:( f:( a a   2). 2).
Thm* ( i: i: a. P(i) a. P(i)   f(i) = 1 f(i) = 1   2) 2)   ({x: ({x: a| P(x) } ~ a| P(x) } ~  (Msize(f))) (Msize(f))) | [card_st_vs_msize] |
Thm* (  ( ( a onto a onto  b)) b))   b b a a | [surj_typing_imp_le] |
Thm* (  ( ( a onto a onto  b)) b))   ( (  ( ( b inj b inj  a)) a)) | [nsub_surj_imp_a_rev_inj2] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)
Thm*  
Thm* ( a: a: , f:( , f:( a onto a onto B). ( B). ( y.least x: y.least x: . (f(x)) e y) . (f(x)) e y)  B inj B inj  a) a) | [nsub_surj_imp_a_rev_inj_gen] |
Thm* Dedekind-Infinite(A)    Finite(A) Finite(A) | [dedekind_imp_nonfin] |
Thm* Dedekind-Infinite(A)   Unbounded(A) Unbounded(A) | [dededing_imp_unb_inf] |
Thm* Dedekind-Infinite(A)   Infinite(A) Infinite(A) | [dedekind_inf_imp_inf] |
Thm* InvFuns(A;A;f;g)   ( ( i: i: . InvFuns(A;A;f{ . InvFuns(A;A;f{ i};g{ i};g{ i})) i})) | [compose_iter_inverses] |
Thm* Bij(A; A; f)   ( ( i: i: . Bij(A; A; f{ . Bij(A; A; f{ i})) i})) | [compose_iter_bijection] |
Thm* Surj(A; A; f)   ( ( i: i: . Surj(A; A; f{ . Surj(A; A; f{ i})) i})) | [compose_iter_surjection] |
Thm* Inj(A; A; f)   ( ( i: i: . Inj(A; A; f{ . Inj(A; A; f{ i})) i})) | [compose_iter_injection] |
Thm*  x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i . k = i j j   f{ f{ i}{ i}{ j}(x) = f{ j}(x) = f{ k}(x) k}(x)  A A | [compose_iter_prod] |
Thm*  f:(A f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i} o f{ i} o f{ j} = f{ j} = f{ k} k} | [compose_iter_sum_comp] |
Thm*  x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i+j . k = i+j   f{ f{ i}(f{ i}(f{ j}(x)) = f{ j}(x)) = f{ k}(x) k}(x) | [compose_iter_sum] |
Thm*  f:(A f:(A  A), u:A. f(u) = u A), u:A. f(u) = u   ( ( i: i: . f{ . f{ i}(u) = u) i}(u) = u) | [compose_iter_point_id] |
Thm*  a,b: a,b: . (A ~ . (A ~  a) a)   (B ~ (B ~  b) b)   ((A ((A B) ~ B) ~  (a (a b)) b)) | [finite_indep_sum_card] |
Thm*  a,b,c: a,b,c: . a . a b = c b = c   (( (( a a  b) ~ b) ~  c) c) | [nsub_mul] |
Thm*  c,a,b: c,a,b: . a+b = c . a+b = c     (( (( a+ a+ b) ~ b) ~  c) c) | [nsub_add] |
Thm*  a,b',b: a,b',b: . b = b'+1 . b = b'+1   ({a...b'} ~ {a..b ({a...b'} ~ {a..b }) }) | [intiseg_intseg] |
Thm*  c,a: c,a: , b: , b: . c = b-a . c = b-a   ({a..b ({a..b } ~ } ~  c) c) | [nsub_intseg] |
Thm*  a,b,a',b': a,b,a',b': . b-a = b'-a' . b-a = b'-a'   ({a..b ({a..b } ~ {a'..b' } ~ {a'..b' }) }) | [intseg_shift] |
Thm*  a,b: a,b: . b . b a a   (Void ~ {a..b (Void ~ {a..b }) }) | [intseg_void] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A ((A  B) ~ (A' B) ~ (A'  B')) B')) | [function_functionality_wrt_one_one_corr] |
Thm*  B,B':(A B,B':(A  Type). ( Type). ( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   ((x:A ((x:A  B(x)) ~ (x:A B(x)) ~ (x:A  B'(x))) B'(x))) | [function_functionality_wrt_one_one_corr_B] |
Thm* (x:A. B(x)) ~ (x:A'. B'(x))   ((x:A ((x:A  B(x)) ~ (x:A' B(x)) ~ (x:A'  B'(x))) B'(x))) | [card_pi] |
Thm*  a,b: a,b: , B:({a..b , B:({a..b } }  Type). Type).
Thm* a<b   ((i:{a..b ((i:{a..b } } B(i)) ~ ((i:{a..(b-1) B(i)) ~ ((i:{a..(b-1) } } B(i))+B(b-1))) B(i))+B(b-1))) | [card_split_end_sum_intseg_family] |
Thm* ( x:A. Dec( x:A. Dec(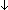 P(x))) P(x)))   (A ~ ({x:A| P(x) }+{x:A| (A ~ ({x:A| P(x) }+{x:A|  P(x) })) P(x) })) | [card_split_decbl_squash] |
Thm*  B:(A B:(A  Type), P:(A Type), P:(A  Prop). Prop).
Thm* ( i:A. Dec(P(i))) i:A. Dec(P(i)))
Thm*  
Thm* ((i:A B(i)) ~ ((i:{i:A| P(i) } B(i)) ~ ((i:{i:A| P(i) } B(i))+(i:{i:A| B(i))+(i:{i:A|  P(i) } P(i) } B(i)))) B(i)))) | [card_split_sigma_dom_decbl] |
Thm* ( x:A. Dec(P(x))) x:A. Dec(P(x)))   (A ~ ({x:A| P(x) }+{x:A| (A ~ ({x:A| P(x) }+{x:A|  P(x) })) P(x) })) | [card_split_decbl] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A ((A B) ~ (A' B) ~ (A' B')) B')) | [product_functionality_wrt_one_one_corr] |
Thm*  B,B':(A B,B':(A  Type). ( Type). ( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   ((x:A ((x:A B(x)) ~ (x:A B(x)) ~ (x:A B'(x))) B'(x))) | [product_functionality_wrt_one_one_corr_B] |
Thm* (x:A. B(x)) ~ (x:A'. B'(x))   ((x:A ((x:A B(x)) ~ (x:A' B(x)) ~ (x:A' B'(x))) B'(x))) | [card_sigma] |
Thm* ( x:A. x:A. 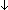 B(x) B(x)   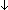 B'(x)) B'(x))   ({x:A| B(x) } ~ {x:A| B'(x) }) ({x:A| B(x) } ~ {x:A| B'(x) }) | [set_functionality_wrt_one_one_corr_n_pred] |
Thm* ( x:A. B(x) x:A. B(x)   B'(x)) B'(x))   ({x:A| B(x) } ~ {x:A| B'(x) }) ({x:A| B(x) } ~ {x:A| B'(x) }) | [set_functionality_wrt_one_one_corr_n_pred2] |
Thm* Bij(A; A'; f)
Thm*  
Thm* ( x:A. x:A. 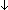 B(x) B(x)   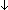 B'(f(x))) B'(f(x)))   ({x:A| B(x) } ~ {x:A'| B'(x) }) ({x:A| B(x) } ~ {x:A'| B'(x) }) | [card_settype_sq] |
Thm* Bij(A; A'; f)
Thm*  
Thm* ( x:A. B(x) x:A. B(x)   B'(f(x))) B'(f(x)))   ({x:A| B(x) } ~ {x:A'| B'(x) }) ({x:A| B(x) } ~ {x:A'| B'(x) }) | [card_settype] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A+B) ~ (A'+B')) ((A+B) ~ (A'+B')) | [union_functionality_wrt_one_one_corr] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   (:A. B) ~ (:A'. B') (:A. B) ~ (:A'. B') | [one_one_corr_fams_indep_if_one_one_corr] |
Thm*  g:(A' g:(A'  A). Bij(A'; A; g) A). Bij(A'; A; g)   (x:A. B(x)) ~ (x':A'. B(g(x'))) (x:A. B(x)) ~ (x':A'. B(g(x'))) | [one_one_corr_fams_if_bij_A] |
Thm* ( x:A. B(x) ~ B'(x)) x:A. B(x) ~ B'(x))   (x:A. B(x)) ~ (x:A. B'(x)) (x:A. B(x)) ~ (x:A. B'(x)) | [one_one_corr_fams_if_one_one_corr_B] |
Thm*  f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) | [bij_imp_exists_inv2] |
Thm*  P:(A P:(A  B B  Prop). ( Prop). ( x:A. x:A.  !y:B. P(x;y)) !y:B. P(x;y))   (A ~ (y:B (A ~ (y:B {x:A| P(x;y) })) {x:A| P(x;y) })) | [partition_type] |
Thm* (A ~  m) m)   (A ~ (A ~  k) k)   m = k m = k | [counting_is_unique] |
Thm* ( A:Type. A:Type.  Finite(A) Finite(A)   Infinite(A)) Infinite(A))   ( ( D:Type. D:Type.   ( (  D) D)   ( (  D)) D)) | [absurd_nonfinite_imp_infinite] |
Thm* ( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A))   ( ( P:Prop. P:Prop.   P P   P) P) | [nonfin_eqv_unb_inf_iff_negnegelim] |
Thm* ( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A))   ( ( D:Type. D:Type.   ( (  D) D)   ( (  D)) D)) | [absurd_nonfin_imp_unb_inf] |
Thm* ( P:Prop. P:Prop.   P P   P) P)   ( ( A:Type. A:Type.  Finite(A) Finite(A)   Unbounded(A)) Unbounded(A)) | [negnegelim_imp_notfin_imp_unb_inf] |
Thm* (A ~ B)   Infinite(A) Infinite(A)   Infinite(B) Infinite(B) | [ooc_preserves_infiniteness] |
Thm* (A ~ B)   Unbounded(A) Unbounded(A)   Unbounded(B) Unbounded(B) | [ooc_preserves_unb_inf] |
Thm* Infinite(A)    Finite(A) Finite(A) | [infinite_imp_nonfinite] |
Thm* Unbounded(A)    Finite(A) Finite(A) | [unb_inf_not_fin] |
Thm*  f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) | [bij_imp_exists_inv_version2] |
Thm*  f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) | [fun_with_inv_is_bij_version2] |
Thm* InvFuns(A;B;f;g)   Bij(B; A; g) Bij(B; A; g) | [fun_with_inv2_is_bij_rev] |
Thm* InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) | [fun_with_inv2_is_bij] |
Thm* (A   C) C)   (B (B   D) D)   A & B A & B   C & D C & D | [parallel_conjunct_imp] |
Thm*  g:(B g:(B  A). Surj(A; B; f) A). Surj(A; B; f)   ( ( x:A. g(f(x)) = x) x:A. g(f(x)) = x)   ( ( y:B. f(g(y)) = y) y:B. f(g(y)) = y) | [left_inv_of_surj_is_right_inv] |
Thm* InvFuns(A;B;f;g)   InvFuns(A;B;f;h) InvFuns(A;B;f;h)   g = h g = h | [inv_funs_2_unique] |
Thm* (A ~ B)   (B ~ C) (B ~ C)   (A ~ C) (A ~ C) | [one_one_corr_2_transitivity] |
Thm* (A ~ B)   (B ~ A) (B ~ A) | [one_one_corr_2_inversion] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A ~ B) ((A ~ B)   (A' ~ B')) (A' ~ B')) | [one_one_corr_2_functionality_wrt_one_one_corr] |
Thm* (A ~ B)   (( ((  A) A)   ( (  B)) B)) | [inhabited_functionality_wrt_one_one_corr] |
Thm* (A ~ B)   (A (A   B) B) | [iff_weakening_wrt_one_one_corr_2] |
Thm* InvFuns(A;B;f;g)   Surj(B; A; g) Surj(B; A; g) | [fun_with_inv2_is_surj_rev] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A inj ((A inj B) ~ (A' inj B) ~ (A' inj B')) B')) | [injection_type_functionality_wrt_ooc] |
Thm* InvFuns(A;B;f;g)   Inj(A; B; f) & Inj(B; A; g) Inj(A; B; f) & Inj(B; A; g) | [invfuns_are_inj] |
Thm* (A ~ B)   Dedekind-Infinite(A) Dedekind-Infinite(A)   Dedekind-Infinite(B) Dedekind-Infinite(B) | [ooc_preserves_dededkind_inf] |
Thm* InvFuns(A;B;f;g)   Inj(B; A; g) Inj(B; A; g) | [fun_with_inv2_is_inj_rev] |
Thm*  B:(A B:(A  Type), B':(A' Type), B':(A'  Type). Type).
Thm* (x:A. B(x)) ~ (x':A'. B'(x'))   (x':A'. B'(x')) ~ (x:A. B(x)) (x':A'. B'(x')) ~ (x:A. B(x)) | [one_one_corr_fams_sym] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A onto ((A onto B) ~ (A' onto B) ~ (A' onto B')) B')) | [surjection_type_functionality_wrt_ooc] |
Thm* InvFuns(A;B;f;g)   Surj(A; B; f) & Surj(B; A; g) Surj(A; B; f) & Surj(B; A; g) | [invfuns_are_surj] |
Thm* InvFuns(A;B;f;g)   InvFuns(B;A;g;f) InvFuns(B;A;g;f) | [inv_funs_2_sym] |
Thm*  k: k: , B:( , B:( k k  Type), Q:(x: Type), Q:(x: k k  B(x) B(x)  Prop). Prop).
Thm* ( x: x: k. k.  y:B(x). Q(x;y)) y:B(x). Q(x;y))   ( ( f:(x: f:(x: k k  B(x)). B(x)).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) | [dep_finite_choice] |
Thm*  k: k: , Q:( , Q:( k k  A A  Prop). Prop).
Thm* ( x: x: k. k.  y:A. Q(x;y)) y:A. Q(x;y))   ( ( f:( f:( k k  A). A).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) | [finite_choice] |
Thm* ( x:A. Dec(P(x))) x:A. Dec(P(x)))
Thm*  
Thm* ((x:A  B(x)) ~ ((x:A st P(x) B(x)) ~ ((x:A st P(x)  B(x)) B(x)) (x:A st (x:A st  P(x) P(x)  B(x)))) B(x)))) | [card_split_prod_intseg_family_decbl] |
Thm* Bij(A; B; g)   Bij(B; C; f) Bij(B; C; f)   Bij(A; C; f o g) Bij(A; C; f o g) | [comp_preserves_bij] |
Thm*  A:Type, A',A'':Type, B:(A A:Type, A',A'':Type, B:(A  Type), B':(A' Type), B':(A'  Type), B'':(A'' Type), B'':(A''  Type). Type).
Thm* (x:A. B(x)) ~ (x':A'. B'(x'))
Thm*  
Thm* (x':A'. B'(x')) ~ (x'':A''. B''(x''))   (x:A. B(x)) ~ (x'':A''. B''(x'')) (x:A. B(x)) ~ (x'':A''. B''(x'')) | [one_one_corr_fams_trans] |
Thm* (A ~ A')   (B ~ B') (B ~ B')   ((A ((A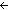  B) ~ (A' B) ~ (A'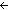  B')) B')) | [inv_pair_functionality_wrt_one_one_corr] |
Thm*  f:(A onto f:(A onto B), a: B), a: . .  a onto a onto A A   (B Discrete) (B Discrete)   Surj(A; B; f) Surj(A; B; f) | [surjection_type_surjection] |
Thm* Surj(A; B; g)   Surj(B; C; f) Surj(B; C; f)   Surj(A; C; f o g) Surj(A; C; f o g) | [comp_preserves_surj] |
Thm* Inj(A; B; g)   Inj(B; C; f) Inj(B; C; f)   Inj(A; C; f o g) Inj(A; C; f o g) | [comp_preserves_inj] |
Thm* Infinite(A)   Unbounded(A) Unbounded(A) | [unboundedly_imp_productively_infinite] |
Thm*  k,n: k,n: . k = n+1 . k = n+1   k! = k k! = k n! n!   | [factorial_via_intseg_step] |
Thm*  P:{P:( P:{P:(   Prop)| Prop)|  i: i: . P(i) }. . P(i) }.
Thm* ( i: i: . Dec(P(i))) . Dec(P(i)))   ( (  {i: {i: | P(i) & ( | P(i) & ( j: j: . j<i . j<i    P(j)) }) P(j)) }) | [least_exists2] |
Thm*  k: k: , P:{P:( , P:{P:( k k  Prop)| Prop)|  i: i: k. P(i) }. k. P(i) }.
Thm* ( i: i: k. Dec(P(i))) k. Dec(P(i)))   ( (  {i: {i: k| P(i) & ( k| P(i) & ( j: j: i. i.  P(j)) }) P(j)) }) | [least_exists] |
Thm*  a,a': a,a': . a'-a = 1 . a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type). (i:{a..a' Type). (i:{a..a' } } B(i)) ~ B(a)) B(i)) ~ B(a)) | [card_sum_family_intseg_singleton_elim] |
Thm* A = B   (A ~ B) (A ~ B) | [one_one_corr_2_weakening_wrt] |
Thm*  a,a': a,a': . a'-a = 1 . a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type). (i:{a..a' Type). (i:{a..a' } }  B(i)) ~ B(a)) B(i)) ~ B(a)) | [card_prod_family_intseg_singleton_elim] |
Thm*  k: k: , j: , j: k, m: k, m: . m = k-1 . m = k-1   ({i: ({i: k| k|  i = j } ~ i = j } ~  m) m) | [nsub_delete] |
Thm*  a,a': a,a': . .
Thm* a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type). (i:{a..a' Type). (i:{a..a' } } B(i)) ~ ({a: B(i)) ~ ({a: } } B(a))) B(a))) | [card_sum_family_singleton_vs_intseg] |
Thm*  R:(A R:(A  A A  Prop). Prop).
Thm* (  A) & (Trans x,y:A. R(x;y)) & ( A) & (Trans x,y:A. R(x;y)) & ( x:A. x:A.  y:A. R(x;y)) y:A. R(x;y))
Thm*  
Thm* ( k: k:  . .  f:( f:( k k  A). A).  i,j: i,j: k. i<j k. i<j   R(f(i);f(j))) R(f(i);f(j))) | [no_finite_model_lemma] |
Thm* (A ~ B)   Finite(A) Finite(A)   Finite(B) Finite(B) | [ooc_preserves_finiteness] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. f(least x: B), y:B. f(least x: . (f(x)) e y) = y) . (f(x)) e y) = y) | [nsub_surj_least_preimage_works_gen] |
Thm*  e:(B e:(B  B B   ). ).
Thm* IsEqFun(B;e)   ( ( a: a: , f:( , f:( a onto a onto B), y:B. (least x: B), y:B. (least x: . (f(x)) e y) . (f(x)) e y)   a) a) | [nsub_surj_least_preimage_total_gen] |
Thm* (A Discrete)   ( ( k: k: , f:( , f:( k inj k inj A). f A). f   k bij k bij {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) | [nsub_inj_discr_range_bijtype] |
Thm* (A Discrete)
Thm*  
Thm* ( k: k: , f:( , f:( k inj k inj A). A).
Thm* ({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
Thm* (& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
Thm* (& Bij( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) | [nsub_inj_discr_range_bij] |
Thm* (A Discrete)   ( ( k: k: , f:( , f:( k k  A). f A). f   k onto k onto {a:A| {a:A|  i: i: k. a = f(i) }) k. a = f(i) }) | [nsub_discr_range_surjtype] |
Thm* (A Discrete)
Thm*  
Thm* ( k: k: , f:( , f:( k k  A). A).
Thm* ({a:A|  i: i: k. a = f(i) } k. a = f(i) }  Type Type
Thm* (& f   k k  {a:A| {a:A|  i: i: k. a = f(i) } k. a = f(i) }
Thm* (& Surj( k; {a:A| k; {a:A|  i: i: k. a = f(i) }; f)) k. a = f(i) }; f)) | [nsub_discr_range_surj] |
Thm*  p:{p:( p:{p:(    )| )|  i: i: . p(i) }. . p(i) }.
Thm* (least i: . p(i)) . p(i))  {i: {i: | p(i) & ( | p(i) & ( j: j: . j<i . j<i    p(j)) } p(j)) } | [least_characterized2] |
Thm* InvFuns(A;B;f;g)   Surj(A; B; f) Surj(A; B; f) | [fun_with_inv2_is_surj] |
Thm* InvFuns(A;B;f;g)   Inj(A; B; f) Inj(A; B; f) | [fun_with_inv2_is_inj] |
Thm* A = A'   B = B' B = B'   (A ~ B) = (A' ~ B') (A ~ B) = (A' ~ B') | [one_one_corr_2_functionality_wrt_eq] |
Thm*  m,k: m,k: , f:( , f:( m m   k). k<m k). k<m   ( ( x,y: x,y: m. x m. x 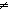 y & f(x) = f(y)) y & f(x) = f(y)) | [pigeon_hole] |
Thm*  m,k: m,k: , f:( , f:( m m   k). Inj( k). Inj( m; m;  k; f) k; f)   m m k k | [inj_imp_le2] |
Thm* (  ( ( m inj m inj  k)) k))   m m k k | [inj_typing_imp_le] |
Thm* ( f:( f:( m m   k). Inj( k). Inj( m; m;  k; f)) k; f))   m m k k | [inj_imp_le] |
Thm*  m: m: , f:( , f:( m m   ). ).  Inj( Inj( m; m;  ; f) ; f)   ( ( x: x: m, y: m, y: x. f(x) = f(y)) x. f(x) = f(y)) | [finite_inj_counter_example] |
Thm* Bij( (m+1); (m+1);  (k+1); f) (k+1); f)   Bij( Bij( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) | [delete_fenum_value_is_fenum] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)   Inj( Inj( m; m;  k; Replace value k by f(m) in f) k; Replace value k by f(m) in f) | [delete_fenum_value_is_inj] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
Thm*  
Thm* ( i: i: m. m.  f(i) = k f(i) = k   (Replace value k by f(m) in f)(i) = f(i) (Replace value k by f(m) in f)(i) = f(i)   k) k) | [delete_fenum_value_comp2] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)
Thm*  
Thm* ( i: i: m. f(i) = k m. f(i) = k   (Replace value k by f(m) in f)(i) = f(m) (Replace value k by f(m) in f)(i) = f(m)   k) k) | [delete_fenum_value_comp1] |
Thm* Inj( (m+1); (m+1);  (k+1); f) (k+1); f)   (Replace value k by f(m) in f) (Replace value k by f(m) in f)   m m   k k | [delete_fenum_value_wf] |
Thm* Bij({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
Thm* (Bij({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
Thm* (Bij(Replace value k by f(m) in f)) | [delete_fenum_value_is_fenum_gen] |
Thm* Inj({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
Thm* (Inj({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
Thm* (Inj(Replace value k by f(m) in f)) | [delete_fenum_value_is_inj_gen] |
Thm* Inj({u: | P(u) }; {v: | P(u) }; {v: | Q(v) }; f) | Q(v) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
Thm* ((Replace value k by f(m) in f)
Thm* ( {u: {u: | P(u) & | P(u) &  u = m } u = m }  {v: {v: | Q(v) & | Q(v) &  v = k } v = k }
Thm* (& Inj({u: | P(u) & | P(u) &  u = m }; {v: u = m }; {v: | Q(v) & | Q(v) &  v = k }; v = k };
Thm* (& Inj(Replace value k by f(m) in f)) | [delete_fenum_value_is_inj_genW] |
Thm* Inj({u: | P(u) }; {u: | P(u) }; {u: | Q(u) }; f) | Q(u) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }, i:{u: | Q(v) }, i:{u: | P(u) & | P(u) &  u = m }. u = m }.
Thm* ( f(i) = k f(i) = k
Thm* ( 
Thm* ((Replace value k by f(m) in f)(i) = f(i)  {v: {v: | Q(v) & | Q(v) &  v = k }) v = k }) | [delete_fenum_value_comp2_gen] |
Thm* Inj({u: | P(u) }; {u: | P(u) }; {u: | Q(u) }; f) | Q(u) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }, i:{u: | Q(v) }, i:{u: | P(u) & | P(u) &  u = m }. u = m }.
Thm* (f(i) = k
Thm* ( 
Thm* ((Replace value k by f(m) in f)(i) = f(m)  {v: {v: | Q(v) & | Q(v) &  v = k }) v = k }) | [delete_fenum_value_comp1_gen] |
Thm* Inj({k: | P(k) }; {k: | P(k) }; {k: | Q(k) }; f) | Q(k) }; f)
Thm*  
Thm* ( m:{u: m:{u: | P(u) }, k:{v: | P(u) }, k:{v: | Q(v) }. | Q(v) }.
Thm* ((Replace value k by f(m) in f)
Thm* ( {u: {u: | P(u) & | P(u) &  u = m } u = m }  {v: {v: | Q(v) & | Q(v) &  v = k }) v = k }) | [delete_fenum_value_wf_gen] |
Thm*  ( (  A) A)   ( ( ! ! (A inj (A inj B)) B)) | [inj_from_empty_unique] |
Thm*  a,a': a,a': . .
Thm* a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type). (i:{a..a' Type). (i:{a..a' } } B(i)) =ext ({a: B(i)) =ext ({a: } } B(a))) B(a))) | [exteq_sum_family_singleton_vs_intseg] |
Thm*  a,a': a,a': . .
Thm* a'-a = 1   ( ( B:({a..a' B:({a..a' } }  Type). (i:{a..a' Type). (i:{a..a' } }  B(i)) =ext ({a: B(i)) =ext ({a: } }  B(a))) B(a))) | [exteq_prod_family_singleton_vs_intseg] |
Thm*  a,a': a,a': . a'-a = 1 . a'-a = 1   ({a..a' ({a..a' } =ext {a: } =ext {a: }) }) | [exteq_singleton_vs_intseg] |
Thm*  a,b: a,b: . a . a b b   (b -- a) = b-a (b -- a) = b-a | [ndiff_vs_diff] |
Def 1-1 x A,y A,y B. R(x;y) B. R(x;y)
Def ==  x,x':A, y,y':B. R(x;y) & R(x';y') x,x':A, y,y':B. R(x;y) & R(x';y')   (x = x' (x = x'   y = y') y = y') | [rel_1_1_b] |
Def R is 1-1 ==  x,x':A, y,y':B. R(x,y) & R(x',y') x,x':A, y,y':B. R(x,y) & R(x',y')   (x = x' (x = x'   y = y') y = y') | [rel_1_1] |