{ 
[Info,A:Type]. [L:EClass(A) List]. [es:EO+(Info)]. [e:E].
(
e 
L[index-of-first X in L.e X - 1])
(first-class(L)(e) = L[index-of-first X in L.e X - 1](e))
supposing e first-class(L) }
{ Proof }
Definitions occuring in Statement :
first-class: first-class(L),
eclass-val: X(e),
in-eclass: e X,
eclass: EClass(A[eo; e]),
event-ordering+: EO+(Info),
es-E: E,
select: l[i],
assert: b,
uimplies: b supposing a,
uall: [x:A]. B[x],
and: P Q,
list: type List,
subtract: n - m,
natural_number: $n,
universe: Type,
equal: s = t,
first_index: index-of-first x in L.P[x]
Definitions :
proper-iseg: L1 < L2,
iseg: l1 
l2,
gt: i > j,
map: map(f;as),
fpf-cap: f(x)?z,
sum-map: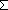 
f[x] for x L,
sum: 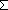(f[x] | x < k),
imax: imax(a;b),
or: P 
Q,
multiply: n * m,
union: left + right,
bool: 
,
length: ||as||,
rationals: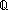 
,
minus: -n,
add: n + m,
real: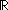 
,
grp_car: |g|,
so_lambda: 
x.t[x],
int: 
,
nat: 
,
fpf-dom: x dom(f),
list_ind: list_ind def,
cand: A c B,
fpf: a:A fp-> B[a],
strong-subtype: strong-subtype(A;B),
le: A B,
ge: i 
j ,
not: 
A,
less_than: a < b,
uiff: uiff(P;Q),
axiom: Ax,
natural_number: $n,
first_index: index-of-first x in L.P[x],
subtract: n - m,
select: l[i],
eclass-val: X(e),
implies: P 
Q,
pair: <a, b>,
void: Void,
false: False,
true: True,
decide: case b of inl(x) => s[x] | inr(y) => t[y],
product: x:A 
B[x],
and: P Q,
nil: [],
first-class: first-class(L),
in-eclass: e X,
set: {x:A| B[x]} ,
prop: 
,
assert: b,
uimplies: b supposing a,
subtype: S 
T,
subtype_rel: A r B,
eq_atom: eq_atom$n(x;y),
atom: Atom,
apply: f a,
top: Top,
es-base-E: es-base-E(es),
token: "$token",
eq_atom: x =a y,
ifthenelse: if b then t else f fi ,
record-select: r.x,
dep-isect: Error :dep-isect,
record+: record+,
event_ordering: EO,
es-E: E,
event-ordering+: EO+(Info),
lambda: x.A[x],
isect: 
x:A. B[x],
function: x:A 
B[x],
all: x:A. B[x],
uall: [x:A]. B[x],
list: type List,
eclass: EClass(A[eo; e]),
so_lambda: x y.t[x; y],
equal: s = t,
universe: Type,
member: t T,
tactic: Error :tactic,
cons: [car / cdr],
cond-class: [X?Y],
isempty: isempty{isempty_compseq_tag_def:o}(e; eo),
ParallelOp: Error :ParallelOp,
RepeatFor: Error :RepeatFor,
CollapseTHEN: Error :CollapseTHEN,
Try: Error :Try,
Unfold: Error :Unfold,
D: Error :D,
Auto: Error :Auto,
so_apply: x[s],
guard: {T},
eq_knd: a = b,
l_member: (x l),
limited-type: LimitedType,
bfalse: ff,
btrue: tt,
eq_bool: p =b q,
lt_int: i <z j,
le_int: i z j,
eq_int: (i =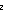
j),
null: null(as),
set_blt: a < b,
grp_blt: a < b,
infix_ap: x f y,
dcdr-to-bool: [d],
bl-all: (xL.P[x])_b,
bl-exists: (
xL.P[x])_b,
b-exists: (i<n.P[i])_b,
eq_type: eq_type(T;T'),
qeq: qeq(r;s),
q_less: q_less(r;s),
q_le: q_le(r;s),
deq-member: deq-member(eq;x;L),
deq-disjoint: deq-disjoint(eq;as;bs),
deq-all-disjoint: deq-all-disjoint(eq;ass;bs),
eq_str: Error :eq_str,
eq_id: a = b,
eq_lnk: a = b,
es-eq-E: e = e',
bimplies: p q,
band: p q,
bor: p q,
bnot: b,
unit: Unit,
isl: isl(x),
can-apply: can-apply(f;x),
rev_implies: P 
Q,
iff: P Q,
sq_type: SQType(T),
tl: tl(l),
hd: hd(l),
sqequal: s ~ t,
int_seg: {i..j
},
MaAuto: Error :MaAuto,
parameter: parm{i}
Lemmas :
first_index_bounds,
length_wf1,
int_subtype_base,
bnot_of_le_int,
select-cons,
le_int_wf,
assert_of_le_int,
bnot_of_lt_int,
assert_functionality_wrt_uiff,
assert_of_lt_int,
is-first-class2,
lt_int_wf,
btrue_wf,
assert_elim,
first_index_cons,
bool_cases,
subtype_base_sq,
bool_subtype_base,
cond-class-val,
rev_implies_wf,
iff_wf,
cond-class_wf,
bool_wf,
iff_weakening_uiff,
eqtt_to_assert,
uiff_transitivity,
eqff_to_assert,
assert_of_bnot,
bnot_wf,
is-cond-class,
in-eclass_wf,
ifthenelse_wf,
false_wf,
assert_wf,
true_wf,
assert_witness,
event-ordering+_wf,
event-ordering+_inc,
subtype_rel_self,
es-base-E_wf,
es-E_wf,
eclass_wf,
es-interface-top,
member_wf,
top_wf,
first-class_wf,
eclass-val_wf,
select_wf,
first_index_wf,
nat_wf,
subtype_rel_wf,
le_wf,
not_wf,
es-interface-subtype_rel,
length_wf_nat
\mforall{}[Info,A:Type]. \mforall{}[L:EClass(A) List]. \mforall{}[es:EO+(Info)]. \mforall{}[e:E].
(\muparrow{}e \mmember{}\msubb{} L[index-of-first X in L.e \mmember{}\msubb{} X - 1])
\mwedge{} (first-class(L)(e) = L[index-of-first X in L.e \mmember{}\msubb{} X - 1](e))
supposing \muparrow{}e \mmember{}\msubb{} first-class(L)
Date html generated:
2011_08_16-AM-11_42_14
Last ObjectModification:
2011_06_20-AM-00_32_57
Home
Index