Nuprl Lemma : Accum-classrel1
 [B,A:
[B,A: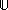 '].
'].  [f:A
[f:A 
 B
B 
 B].
B].  [init:Id
[init:Id 
 bag(B)].
bag(B)].  [X:EClass'(A)].
[X:EClass'(A)].  [es:EO'].
[es:EO'].  [e:E].
[e:E].  [v:B].
[v:B].
uiff(v  Accum-class(f;init;X)(e);
Accum-class(f;init;X)(e);
 L:(A
L:(A  E) List
E) List
(classrel-list(es;A;X;L;e)
 (
(
 null(L))
null(L))
 (e = last(map(
(e = last(map( p.(snd(p));L)))
p.(snd(p));L)))
 (
( x:B
x:B
(bag-member(B;x;init loc(e))
 (v = list_accum(b,a.f a b;x;map(
(v = list_accum(b,a.f a b;x;map( p.(fst(p));L)))))))
p.(fst(p));L)))))))
Proof not projected
Definitions occuring in Statement :
classrel-list: classrel-list(es;A;X;L;e),
Accum-class: Accum-class(f;init;X),
Message: Message,
classrel: v  X(e),
eclass: EClass(A[eo; e]),
event-ordering+: EO+(Info),
es-loc: loc(e),
es-E: E,
Id: Id,
map: map(f;as),
null: null(as),
assert:
X(e),
eclass: EClass(A[eo; e]),
event-ordering+: EO+(Info),
es-loc: loc(e),
es-E: E,
Id: Id,
map: map(f;as),
null: null(as),
assert:  b,
uiff: uiff(P;Q),
uall:
b,
uiff: uiff(P;Q),
uall:  [x:A]. B[x],
pi1: fst(t),
pi2: snd(t),
exists:
[x:A]. B[x],
pi1: fst(t),
pi2: snd(t),
exists:  x:A. B[x],
not:
x:A. B[x],
not:  A,
squash:
A,
squash:  T,
and: P
T,
and: P  Q,
apply: f a,
lambda:
Q,
apply: f a,
lambda:  x.A[x],
function: x:A
x.A[x],
function: x:A 
 B[x],
product: x:A
B[x],
product: x:A  B[x],
list: type List,
universe: Type,
equal: s = t,
list_accum: list_accum(x,a.f[x; a];y;l),
last: last(L),
bag-member: bag-member(T;x;bs),
bag: bag(T)
B[x],
list: type List,
universe: Type,
equal: s = t,
list_accum: list_accum(x,a.f[x; a];y;l),
last: last(L),
bag-member: bag-member(T;x;bs),
bag: bag(T)
Lemmas :
firstn_length,
firstn_append,
firstn_map,
bfalse_wf,
nth_tl_is_nil,
nth_tl_decomp,
nth_tl_map,
list_accum_split,
map_length,
classrel-list-prefix,
listp_wf,
atom2_subtype_base,
es-first_wf,
es-loc-pred,
es-le-loc,
assert_of_lt_int,
iff_weakening_uiff,
iff_functionality_wrt_iff,
iff_imp_equal_bool,
btrue_wf,
lt_int_wf,
select_append,
int_subtype_base,
map_select,
event_ordering_wf,
length-map,
length_append,
length_cons,
length_nil,
es-p-local-pred_wf,
list_subtype_base,
product_subtype_base,
length_zero,
length_wf_nat,
non_neg_length,
gt_wf,
firstn_last,
pair-eta,
firstn_wf,
length_wf1,
last-map,
list_accum_append,
last_append,
not_assert_elim,
null_append,
bool_subtype_base,
band_wf,
es-le_weakening,
cons_member,
primed-class-opt-exists,
es-le-not-locl,
decidable__es-locl,
decidable__es-le,
decidable__es-E-equal,
decidable__l_member,
l_member_subtype,
member_append,
es-locl_irreflexivity,
es-le_weakening_eq,
es-locl_transitivity2,
null_wf,
ifthenelse_wf,
member_singleton,
not_functionality_wrt_iff,
no_repeats-single,
l_disjoint_wf,
map_append_sq,
no_repeats-append,
es-causl_weakening,
es-locl_transitivity1,
member_map,
sorted-by-append,
select_wf,
int_seg_wf,
uall_wf,
iff_transitivity,
l_all_append,
and_functionality_wrt_iff,
rev_implies_wf,
l_all_single,
l_all_wf2,
true_wf,
set_subtype_base,
subtype_base_sq,
pi1_wf,
pos_length2,
l_all_wf,
sorted-by_wf,
es-locl_wf,
no_repeats_wf,
iff_wf,
es-le_wf,
l_member_wf,
append_wf,
primed-class-opt-classrel,
lifting-2_wf,
simple-comb-2-classrel,
primed-class-opt_wf,
rec-combined-class-opt-1_wf,
rec-combined-class-opt-1-classrel,
es-causl_wf,
le_wf,
ge_wf,
nat_properties,
nat_wf,
uiff_wf,
es-causl-swellfnd,
pi1_wf_top,
list_accum_wf,
bool_wf,
null-map,
subtype_rel_wf,
intensional-universe_wf,
false_wf,
es-loc_wf,
pi2_wf,
map_wf,
last_wf,
member_wf,
top_wf,
null_wf3,
subtype_rel_self,
es-base-E_wf,
eclass_wf,
eclass_wf3,
eclass_wf2,
event-ordering+_wf,
event-ordering+_inc,
Id_wf,
bag_wf,
sq_stable__uiff,
sq_stable__classrel,
sq_stable__squash,
classrel_wf,
Message_wf,
Accum-class_wf,
squash_wf,
bag-member_wf,
es-E_wf,
assert_wf,
not_wf,
classrel-list_wf
\mforall{}[B,A:\mBbbU{}']. \mforall{}[f:A {}\mrightarrow{} B {}\mrightarrow{} B]. \mforall{}[init:Id {}\mrightarrow{} bag(B)]. \mforall{}[X:EClass'(A)]. \mforall{}[es:EO']. \mforall{}[e:E]. \mforall{}[v:B].
uiff(v \mmember{} Accum-class(f;init;X)(e);\mdownarrow{}\mexists{}L:(A \mtimes{} E) List
(classrel-list(es;A;X;L;e)
\mwedge{} (\mneg{}\muparrow{}null(L))
\mwedge{} (e = last(map(\mlambda{}p.(snd(p));L)))
\mwedge{} (\mexists{}x:B
(bag-member(B;x;init loc(e))
\mwedge{} (v = list\_accum(b,a.f a b;x;map(\mlambda{}p.(fst(p));L)))))))
Date html generated:
2011_10_20-PM-03_45_52
Last ObjectModification:
2011_08_24-PM-12_47_29
Home
Index