{ 
[Info:Type]. [es:EO+(Info)]. [A,B:Type]. [base:B]. [f:B 
A B].
[X:EClass(A)]. [size:
]. [num:A ]. [P:A 
]. [e:E].
uiff(
e 
Collect(size v's from X with maximum num[v] such that P[v]
initialze x:=base on each v set x:=f[x;v]);(e X)
e is first@ loc(e) s.t. c.||filter(
c.((num[X(c)] =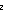
num[X(e)])
P[X(c)]);
(X)(c))||
= size
e'<e.(e' X)
((num[X(e')] num[X(e)])
((num[X(e')] = num[X(e)]) (P[X(e')])))) }
{ Proof }
Definitions occuring in Statement :
es-collect-filter-accum: es-collect-filter-accum,
es-interface-predecessors: (X)(e),
eclass-val: X(e),
in-eclass: e X,
eclass: EClass(A[eo; e]),
event-ordering+: EO+(Info),
es-first-at: e is first@ i s.t. e.P[e],
alle-lt: e<e'.P[e],
es-loc: loc(e),
es-E: E,
length: ||as||,
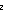eq_int: (i = j),
band: p q,
assert: b,
bool: ,
nat_plus: ,
nat: ,
uiff: uiff(P;Q),
uall: [x:A]. B[x],
so_apply: x[s1;s2],
so_apply: x[s],
le: A B,
implies: P Q,
and: P Q,
lambda: x.A[x],
function: x:A B[x],
int: 
,
universe: Type,
equal: s = t,
filter: filter(P;l)
Definitions :
deq: EqDecider(T),
ma-state: State(ds),
class-program: ClassProgram(T),
isl: isl(x),
can-apply: can-apply(f;x),
eq_id: a = b,
sqequal: s ~ t,
append: as @ bs,
locl: locl(a),
atom: Atom$n,
intensional-universe: IType,
cand: A c B,
Knd: Knd,
IdLnk: IdLnk,
cond-class: [X?Y],
eq_knd: a = b,
fpf-dom: x dom(f),
es-causl: (e < e'),
guard: {T},
btrue: tt,
sq_type: SQType(T),
is_list_splitting: is_list_splitting(T;L;LL;L2;f),
is_accum_splitting: is_accum_splitting(T;A;L;LL;L2;f;g;x),
req: x = y,
rnonneg: rnonneg(r),
rleq: x y,
i-member: r I,
partitions: partitions(I;p),
modulus-of-ccontinuity: modulus-of-ccontinuity(omega;I;f),
fpf-sub: f 
g,
squash: 
T,
sq_stable: SqStable(P),
tag-by: z
T,
fset: FSet{T},
isect2: T1 
T2,
b-union: A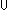 
B,
list: type List,
fpf-cap: f(x)?z,
or: P 
Q,
infix_ap: x f y,
es-collect-accum: es-collect-accum(X;x.num[x];init;a,v.f[a; v];a.P[a]),
es-interface-accum: es-interface-accum(f;x;X),
collect_filter: collect_filter(),
collect_accum: collect_accum(x.num[x];init;a,v.f[a; v];a.P[a]),
es-prior-interface: prior(X),
es-interface-at: X@i,
union: left + right,
exists: 
x:A. B[x],
record: record(x.T[x]),
atom: Atom,
token: "$token",
int_nzero: 
,
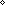real: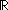 
,
grp_car: |g|,
l_member: (x l),
es-E-interface: E(X),
limited-type: LimitedType,
fpf: a:A fp-> B[a],
top: Top,
so_lambda: 
x.t[x],
strong-subtype: strong-subtype(A;B),
eq_atom: x =a y,
eq_atom: eq_atom$n(x;y),
record-select: r.x,
dep-isect: Error :dep-isect,
record+: record+,
ge: i 
j ,
subtype_rel: A r B,
set: {x:A| B[x]} ,
so_apply: x[s1;s2],
es-collect-filter-accum: es-collect-filter-accum,
in-eclass: e X,
rev_implies: P 
Q,
iff: P Q,
less_than: a < b,
es-locl: (e <loc e'),
es-interface-predecessors: (X)(e),
eclass-val: X(e),
apply: f a,
so_apply: x[s],
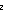eq_int: (i = j),
band: p q,
filter: filter(P;l),
length: ||as||,
int: ,
axiom: Ax,
es-loc: loc(e),
Id: Id,
pair: <a, b>,
le: A B,
not: 
A,
implies: P Q,
alle-lt: e<e'.P[e],
es-first-at: e is first@ i s.t. e.P[e],
void: Void,
false: False,
true: True,
decide: case b of inl(x) => s[x] | inr(y) => t[y],
ifthenelse: if b then t else f fi ,
assert: b,
uimplies: b supposing a,
product: x:A B[x],
and: P Q,
uiff: uiff(P;Q),
bool: ,
nat: ,
nat_plus: ,
subtype: S T,
event_ordering: EO,
es-E: E,
lambda: x.A[x],
so_lambda: x y.t[x; y],
eclass: EClass(A[eo; e]),
all: x:A. B[x],
function: x:A B[x],
isect: x:A. B[x],
uall: [x:A]. B[x],
event-ordering+: EO+(Info),
member: t T,
equal: s = t,
MaAuto: Error :MaAuto,
Try: Error :Try,
CollapseTHEN: Error :CollapseTHEN,
prop: 
,
RepeatFor: Error :RepeatFor,
Complete: Error :Complete,
Auto: Error :Auto,
tactic: Error :tactic,
universe: Type,
nil: [],
do-apply: do-apply(f;x),
minus: -n,
bfalse: ff,
it: 
,
inr: inr x ,
inl: inl x ,
spreadn: spread4,
es-filter-image: f[X],
p-outcome: Outcome,
rationals: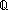 
,
natural_number: $n,
spread: spread def,
add: n + m,
list_accum_pair: list_accum_pair(a,x.f[a; x];b,x.g[b; x];a0;b0;L),
spreadn: spread3,
list_accum: list_accum(x,a.f[x; a];y;l),
bl-all: (xL.P[x])_b,
pi2: snd(t),
pi1: fst(t),
bnot: b,
bor: p q,
eq_bool: p =b q,
null: null(as),
set_blt: a < b,
grp_blt: a < b,
dcdr-to-bool: [d],
bl-exists: (xL.P[x])_b,
b-exists: (i<n.P[i])_b,
eq_type: eq_type(T;T'),
qeq: qeq(r;s),
q_less: q_less(r;s),
q_le: q_le(r;s),
deq-member: deq-member(eq;x;L),
deq-disjoint: deq-disjoint(eq;as;bs),
deq-all-disjoint: deq-all-disjoint(eq;ass;bs),
eq_str: Error :eq_str,
eq_lnk: a = b,
es-eq-E: e = e',
bimplies: p q,
lt_int: i <z j,
le_int: i z j,
unit: Unit,
int_eq: if a=b then c else d,
collect-event: collect-event(es;X;n;v.num[v];L.P[L];e),
mapfilter: mapfilter(f;P;L),
D: Error :D,
THENM: Error :THENM,
CollapseTHENA: Error :CollapseTHENA,
l_all: (xL.P[x]),
Subst': Error :Subst',
RepUR: Error :RepUR,
cons: [car / cdr],
uni_sat: a = !x:T. Q[x],
inv_funs: InvFuns(A;B;f;g),
inject: Inj(A;B;f),
eqfun_p: IsEqFun(T;eq),
refl: Refl(T;x,y.E[x; y]),
urefl: UniformlyRefl(T;x,y.E[x; y]),
sym: Sym(T;x,y.E[x; y]),
usym: UniformlySym(T;x,y.E[x; y]),
trans: Trans(T;x,y.E[x; y]),
utrans: UniformlyTrans(T;x,y.E[x; y]),
anti_sym: AntiSym(T;x,y.R[x; y]),
uanti_sym: UniformlyAntiSym(T;x,y.R[x; y]),
connex: Connex(T;x,y.R[x; y]),
uconnex: uconnex(T; x,y.R[x; y]),
coprime: CoPrime(a,b),
ident: Ident(T;op;id),
assoc: Assoc(T;op),
comm: Comm(T;op),
inverse: Inverse(T;op;id;inv),
bilinear: BiLinear(T;pl;tm),
bilinear_p: IsBilinear(A;B;C;+a;+b;+c;f),
action_p: IsAction(A;x;e;S;f),
dist_1op_2op_lr: Dist1op2opLR(A;1op;2op),
fun_thru_1op: fun_thru_1op(A;B;opa;opb;f),
fun_thru_2op: FunThru2op(A;B;opa;opb;f),
cancel: Cancel(T;S;op),
monot: monot(T;x,y.R[x; y];f),
monoid_p: IsMonoid(T;op;id),
group_p: IsGroup(T;op;id;inv),
monoid_hom_p: IsMonHom{M1,M2}(f),
grp_leq: a b,
integ_dom_p: IsIntegDom(r),
prime_ideal_p: IsPrimeIdeal(R;P),
no_repeats: no_repeats(T;l),
value-type: value-type(T),
qabs: |r|,
map: map(f;as),
hd: hd(l),
last: last(L),
remove-repeats: remove-repeats(eq;L),
select: l[i],
ExRepD: Error :ExRepD,
divides: b | a,
assoced: a ~ b,
set_leq: a b,
set_lt: a <p b,
grp_lt: a < b,
l_contains: A B,
reducible: reducible(a),
prime: prime(a),
l_exists: (xL. P[x]),
fun-connected: y is f*(x),
qle: r s,
qless: r < s,
q-rel: q-rel(r;x),
i-finite: i-finite(I),
i-closed: i-closed(I),
fset-member: a s,
f-subset: xs ys,
fset-closed: (s closed under fs),
l_disjoint: l_disjoint(T;l1;l2),
cs-not-completed: in state s, a has not completed inning i,
cs-archived: by state s, a archived v in inning i,
cs-passed: by state s, a passed inning i without archiving a value,
cs-inning-committed: in state s, inning i has committed v,
cs-inning-committable: in state s, inning i could commit v ,
cs-archive-blocked: in state s, ws' blocks ws from archiving v in inning i,
cs-precondition: state s may consider v in inning i,
es-le: e loc e' ,
es-causle: e c e',
existse-before: e<e'.P[e],
existse-le: ee'.P[e],
alle-le: ee'.P[e],
alle-between1: e[e1,e2).P[e],
existse-between1: e[e1,e2).P[e],
alle-between2: e[e1,e2].P[e],
existse-between2: e[e1,e2].P[e],
existse-between3: e(e1,e2].P[e],
es-fset-loc: i locs(s),
es-r-immediate-pred: es-r-immediate-pred(es;R;e';e),
same-thread: same-thread(es;p;e;e'),
decidable: Dec(P),
ParallelOp: Error :ParallelOp,
AssertBY: Error :AssertBY,
es-pred: pred(e),
es-init: es-init(es;e)
Lemmas :
es-causl_weakening,
alle-le_wf,
btrue_neq_bfalse,
es-causle-le,
es-causl_wf,
member-interface-predecessors,
member-interface-predecessors-subtype,
es-le_wf,
es-locl_transitivity1,
es-le_weakening,
and_functionality_wrt_uiff2,
assert_of_band,
and_functionality_wrt_uiff3,
first-at-filter-interface-predecessors1,
decidable_wf,
or_functionality_wrt_uiff,
assert_of_bor,
implies_functionality_wrt_iff,
decidable__assert,
es-first-at-implies-first-at,
member-mapfilter,
eq_int_eq_true,
l_member-settype,
l_member_subtype,
length-map,
list_subtype_base,
filter-sq,
property-from-l_member,
sq_stable_wf,
sq_stable__equal,
list-set-type2,
assert_of_eq_int,
not_functionality_wrt_uiff,
assert-bl-all,
l_all_wf,
l_all_wf2,
isl_wf,
es-collect-accum-val,
collect-event_wf,
is-collect-accum,
mapfilter_wf,
unit_wf,
es-interface-val_wf2,
assert_of_bnot,
eqff_to_assert,
uiff_transitivity,
eqtt_to_assert,
pi2_wf,
pi1_wf_top,
bnot_wf,
bor_wf,
es-collect-accum_wf,
btrue_wf,
nat_properties,
es-is-filter-image,
iff_functionality_wrt_iff,
es-filter-image_wf,
can-apply_wf,
bfalse_wf,
product_subtype_base,
int_subtype_base,
list_accum_wf,
bl-all_wf,
list_accum_pair-sq,
length-as-accum,
bl-all-as-accum,
set_subtype_base,
squash_wf,
es-E-interface_wf,
Id_wf,
eclass-val_wf,
nat_wf,
event-ordering+_inc,
es-E_wf,
eq_int_wf,
band_wf,
es-interface-predecessors_wf,
es-loc_wf,
filter_wf,
length_wf1,
es-first-at_wf,
alle-lt_wf,
assert_wf,
le_wf,
in-eclass_wf,
es-interface-top,
es-collect-filter-accum_wf,
member_wf,
eclass_wf,
assert_witness,
bool_wf,
nat_plus_wf,
event-ordering+_wf,
event_ordering_wf,
subtype_rel_self,
es-interface-subtype_rel2,
top_wf,
subtype_rel_wf,
ifthenelse_wf,
l_member_wf,
record_wf,
record+_wf,
Error :dep-isect_wf,
sq_stable__assert,
subtype_base_sq,
bool_subtype_base,
assert_elim,
length_wf_nat,
es-locl_wf,
false_wf,
true_wf,
not_wf,
rev_implies_wf,
iff_wf,
intensional-universe_wf,
iff_weakening_uiff,
uiff_inversion,
assert-eq-id,
list-subtype,
filter_type,
nat_plus_properties
\mforall{}[Info:Type]. \mforall{}[es:EO+(Info)]. \mforall{}[A,B:Type]. \mforall{}[base:B]. \mforall{}[f:B {}\mrightarrow{} A {}\mrightarrow{} B]. \mforall{}[X:EClass(A)]. \mforall{}[size:\mBbbN{}\msupplus{}].
\mforall{}[num:A {}\mrightarrow{} \mBbbN{}]. \mforall{}[P:A {}\mrightarrow{} \mBbbB{}]. \mforall{}[e:E].
uiff(\muparrow{}e \mmember{}\msubb{} Collect(size v's from X with maximum num[v] such that P[v] initialze x:=base
on each v set x:=f[x;v]);(\muparrow{}e \mmember{}\msubb{} X)
\mwedge{} e is first@ loc(e) s.t. c.||filter(\mlambda{}c.((num[X(c)] =\msubz{} num[X(e)]) \mwedge{}\msubb{} P[X(c)]);\mleq{}(X)(c))|| = size
\mwedge{} \mforall{}e'<e.(\muparrow{}e' \mmember{}\msubb{} X) {}\mRightarrow{} ((num[X(e')] \mleq{} num[X(e)]) \mwedge{} ((num[X(e')] = num[X(e)]) {}\mRightarrow{} (\muparrow{}P[X(e')]))))
Date html generated:
2011_08_16-PM-05_30_32
Last ObjectModification:
2010_11_14-PM-07_34_40
Home
Index